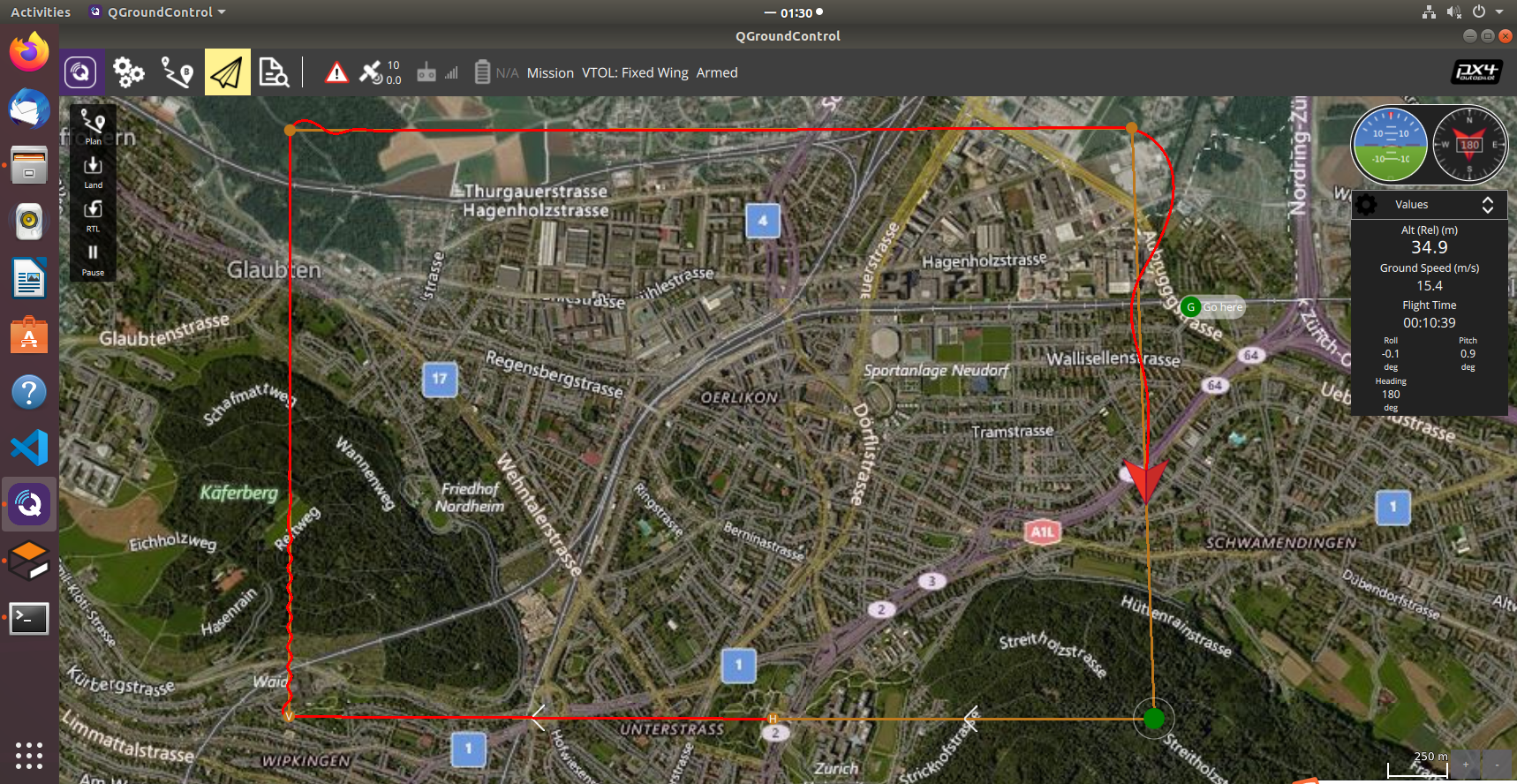
固定翼路径跟踪L1导航算法
当前PX4、Ardupilot中固定翼路径跟随算法主要基于L1导航算法实现
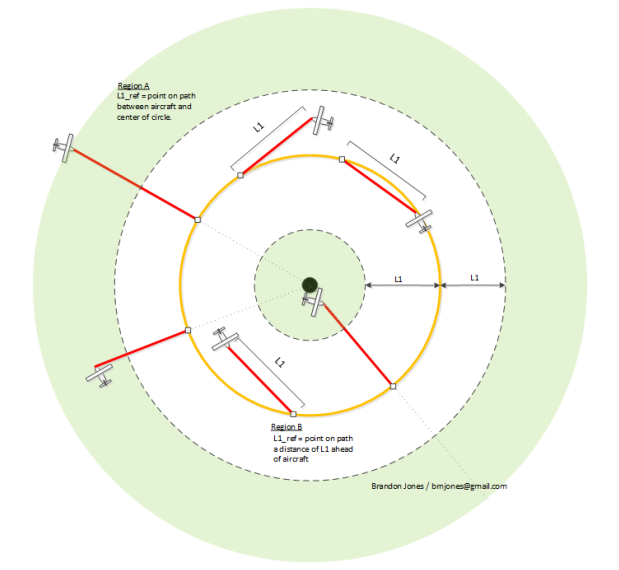
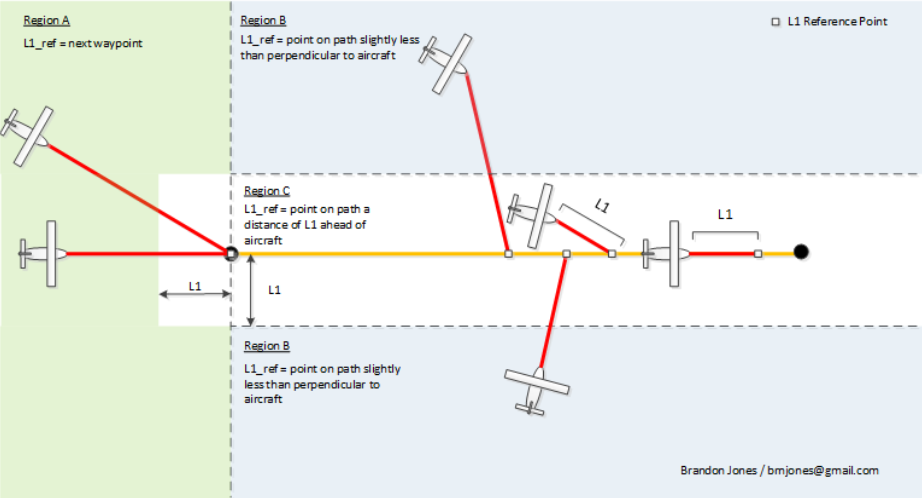
背景
问题:存在目标航点B,期望的航线AB,其中A为上一个航点,B为当前目标航点,飞机位置在P点,如何使飞机一边贴近AB航线一边向B点靠近?
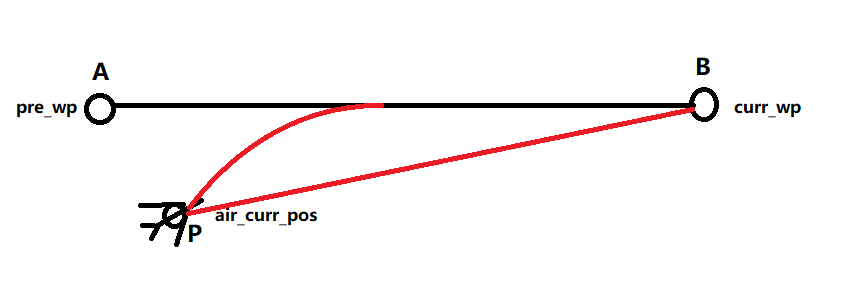
正常飞行中,飞机的位置P应该在AB的连线上,但由于某种扰动(如风的干扰),或者初始条件(飞机起飞时就不在AB航线上)导致飞机偏离了原本的AB航线,此时飞机要飞到B点,有如下两种方式:
- 从当前P点直接朝B点飞行,飞图中直红线
- 逐渐切入AB航线,尽量压着航向飞向B点
实际飞行中,航点的选择可能本身是要绕开部分障碍物,假设P点和B点之间有障碍物,这时直飞B点的方案就不可行了,我们想要飞机尽快切入AB航线,沿着AB航线飞行。L1算法就是解决该问题一个比较好的方案。
符号说明
初探L1制导律
L1制导律在目标路径上选择一个参考点,利用该参考点给出一个横向加速度指令$a{s{cmd}}$来使飞机的潜在路径实时经过参考点。飞机位置和参考点的连线即为L1,这也是L1制导律名字来源。之后的公式和主要图片来源于如下论文:http://acl.mit.edu/papers/gnc_park_deyst_how.pdf
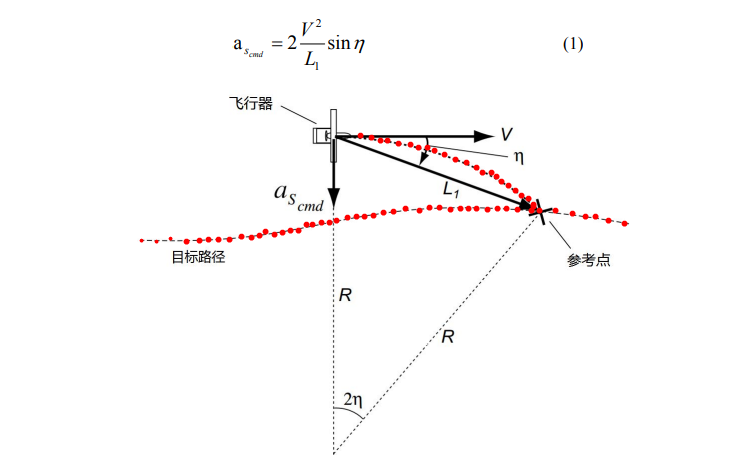
横向加速度计算如下:
通过实时更新参考点位置就可以实时更新来使得飞行器的轨迹逐渐切入目标路径:
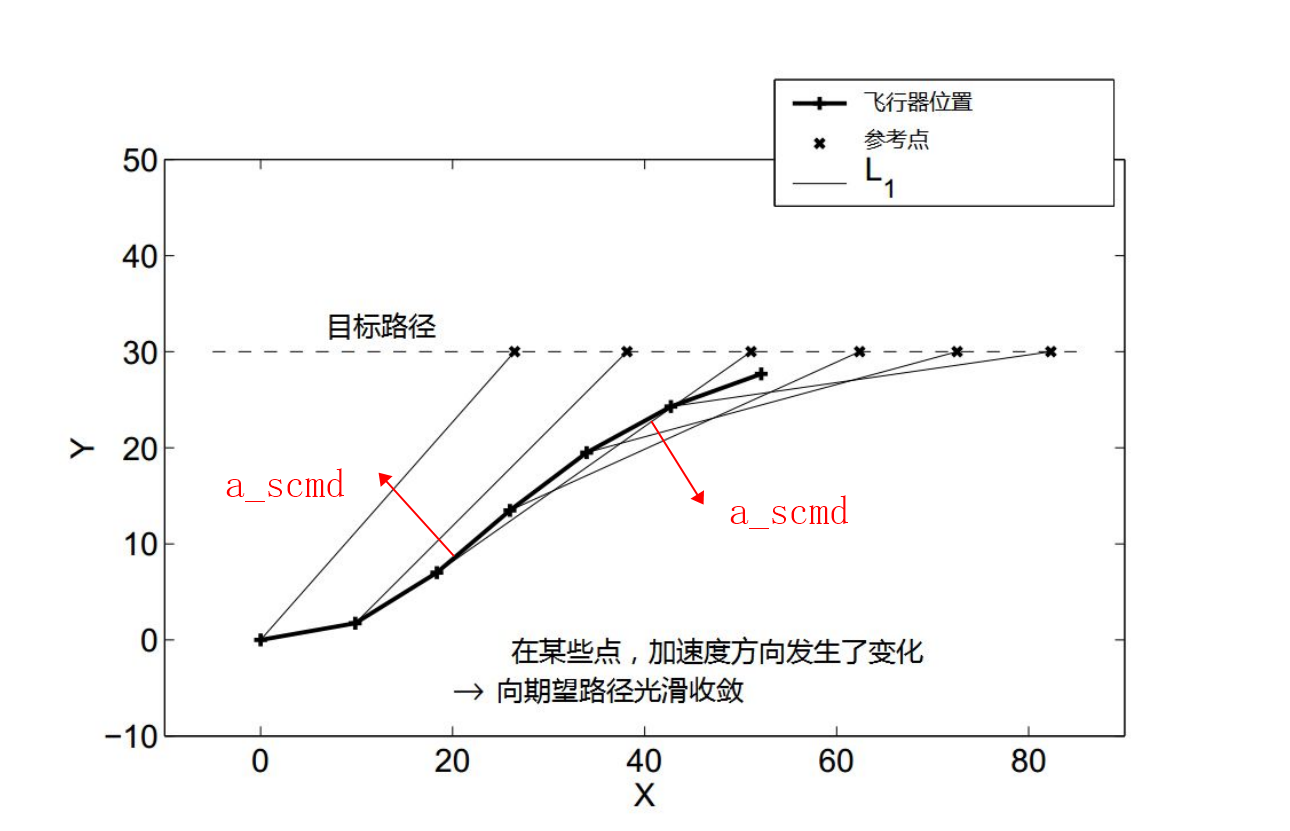
上面的离散点表示中可以看到,飞行器总是趋向于速度方向和L1线段方向对齐,而L1线段逐渐和目标路径对齐,进而间接带动飞行器最终速度方向也和目标路径对齐。最终飞回至直线上去,会变为如下情况:
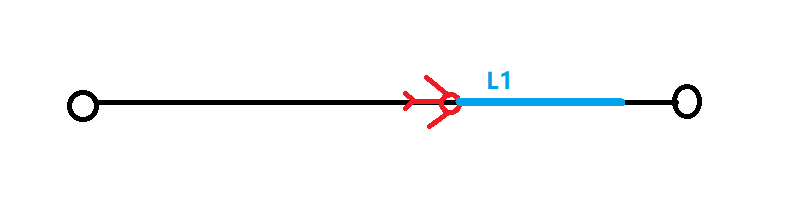
这也可以从加速度方向看出,当$\eta$大于0时,会产生向右加速的指令,来使飞行器速度方向对齐L1,$\eta$小于0时同理。
两种情形下的L1制导律
固定翼实际飞行中的路径跟踪主要可分为两种情况:
- 跟踪一条直线(常见)
- 跟踪一条圆形路径
弹簧质量阻尼系统
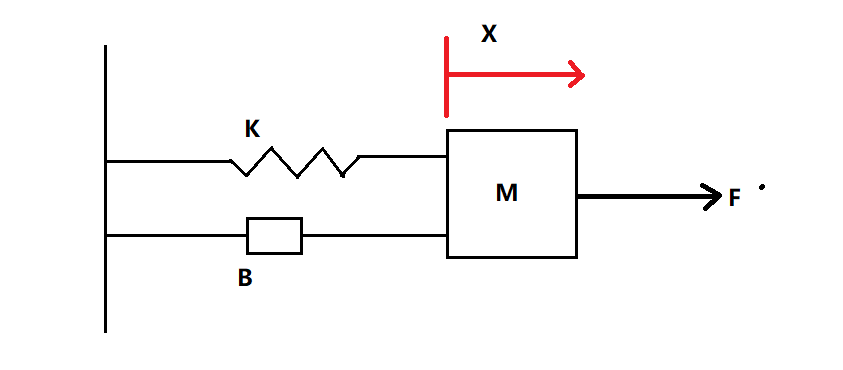
作简单的受力分析可得到:
即:
整理一下:
定义$\omega_n = \sqrt{\frac{K}{m}}$,称为固有频率,$\zeta=\frac{B}{2\sqrt{Km}}$,称为阻尼比,当没有外力时,即F为0,这时上式就可以写成:
该微分方程特征方程为:
得到:
这时,可以分以下几种情况:
$\zeta>1$,此时$0<\sqrt{\zeta^2-1}<\zeta$,$\lambda_1<0,\lambda_2<0$,此时微分方程的解为:$x(t)=C_1e^{\lambda_1t}+C_2e^{\lambda_2t}$,这时$x(t)$是直接收敛的
$\zeta=1$,此时$\lambda=\lambda_1=\lambda_2=-\omega_n$,此时微分方程的解为:$x(t)=(C_1+C_2t)e^{\lambda}t$,此时也是收敛的。
$0<\zeta<1$,此时$\lambda_1=-\zeta\omega_n+i\omega_n\sqrt{1-\zeta^2}$,$\lambda_2=-\zeta\omega_n-i\omega_n\sqrt{1-\zeta^2}$,这是一对共轭复根,此时微分方程的解可以写成:
其中$\omega_d$称为阻尼固有频率。
$\zeta=0$,此时微分方程的解为:$x(t)=\sqrt{C_1^2+C_2^2}sin(\omega_nt+\phi)$,这时一个正弦函数,频率就是无阻尼自然频率$\omega_n$。
$\zeta<0$,发散。
在初始条件不为0时,没有外力输入,则不同的阻尼比会有不同的响应,假设初始的$x=x_0$,$\dot{x}=0$,其实就相当于手将质量块M向右拉动值$x_0$处,然后松手,看$x$如何变化。以阻尼比的不同可有如下响应情况:
- $\zeta>1$,过阻尼:
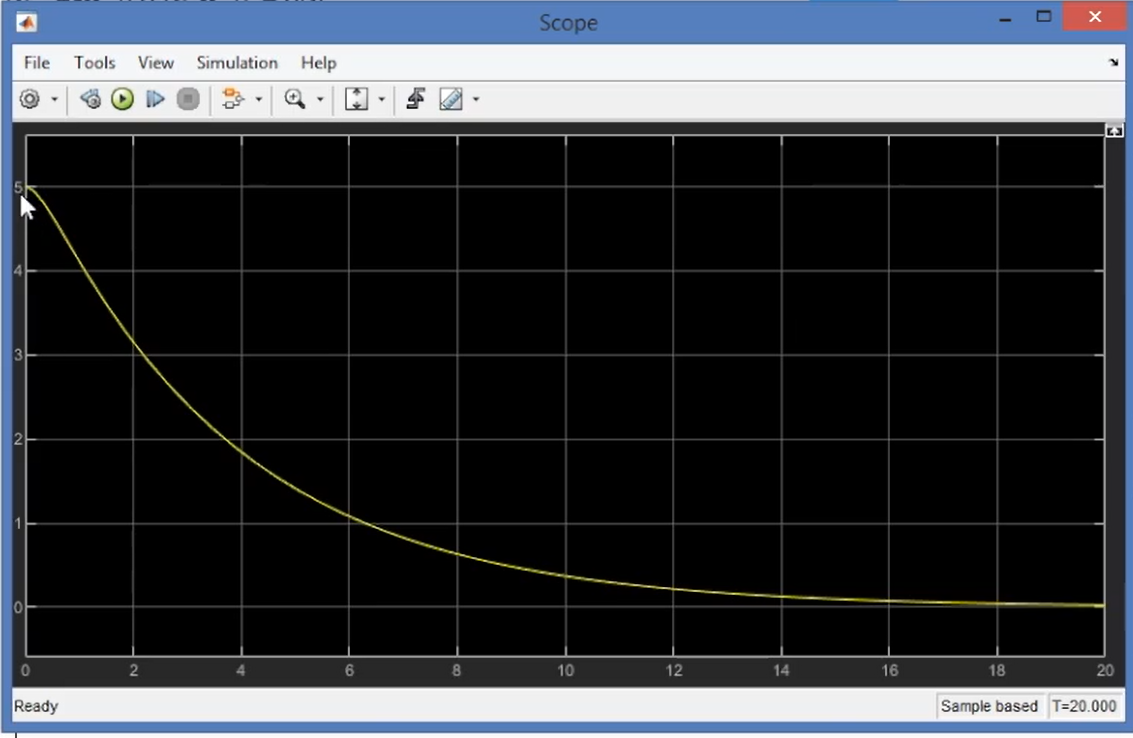
- $\zeta=1$,临界阻尼:
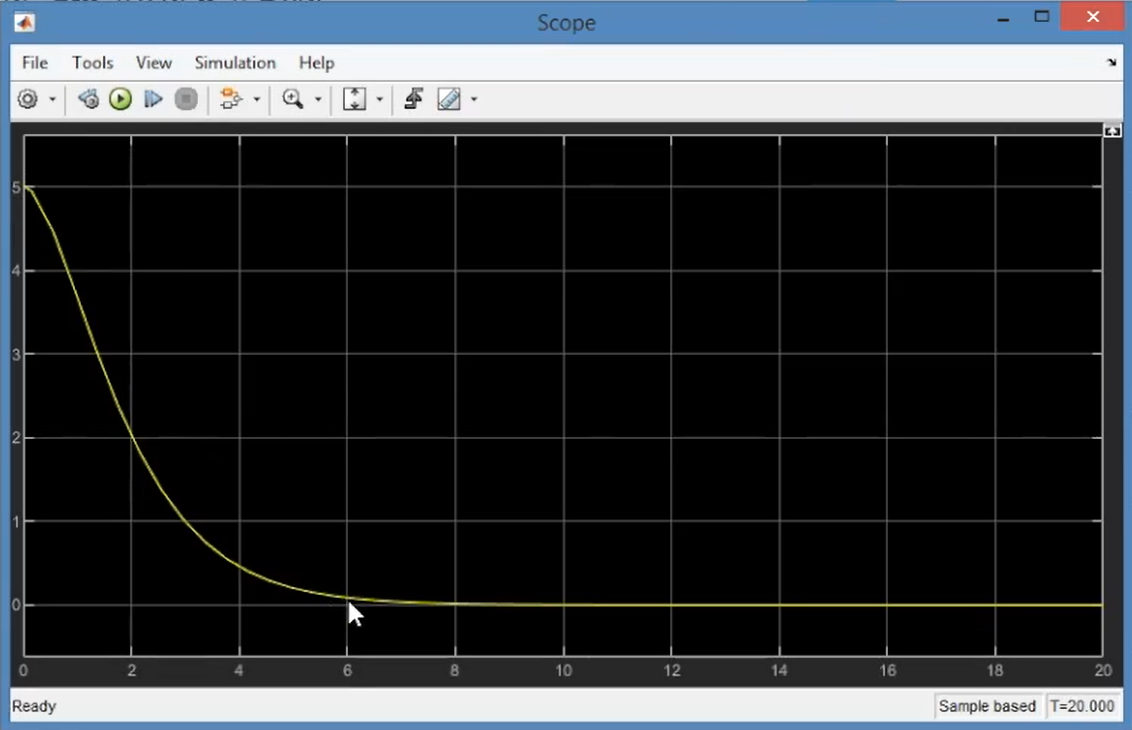
- $0<\zeta<1$,欠阻尼,这个振动的频率就是$\omega_d$:
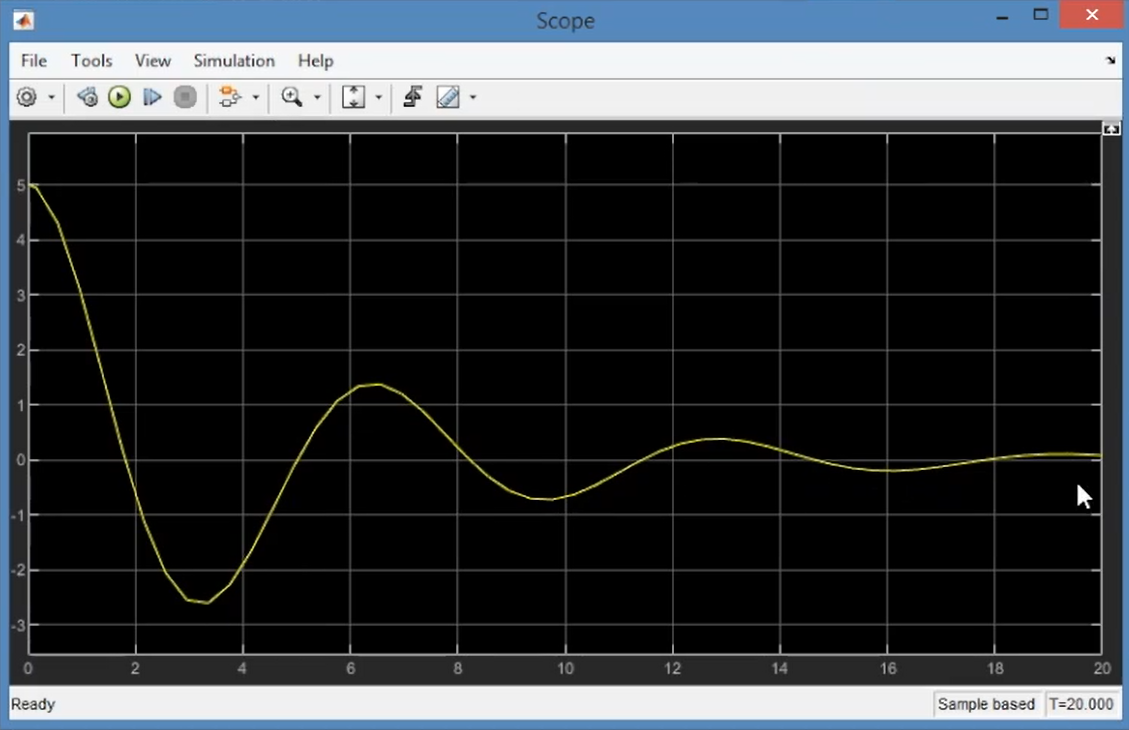
- $\zeta=0$,无阻尼,此时这个正弦的频率就是$\omega_n$:
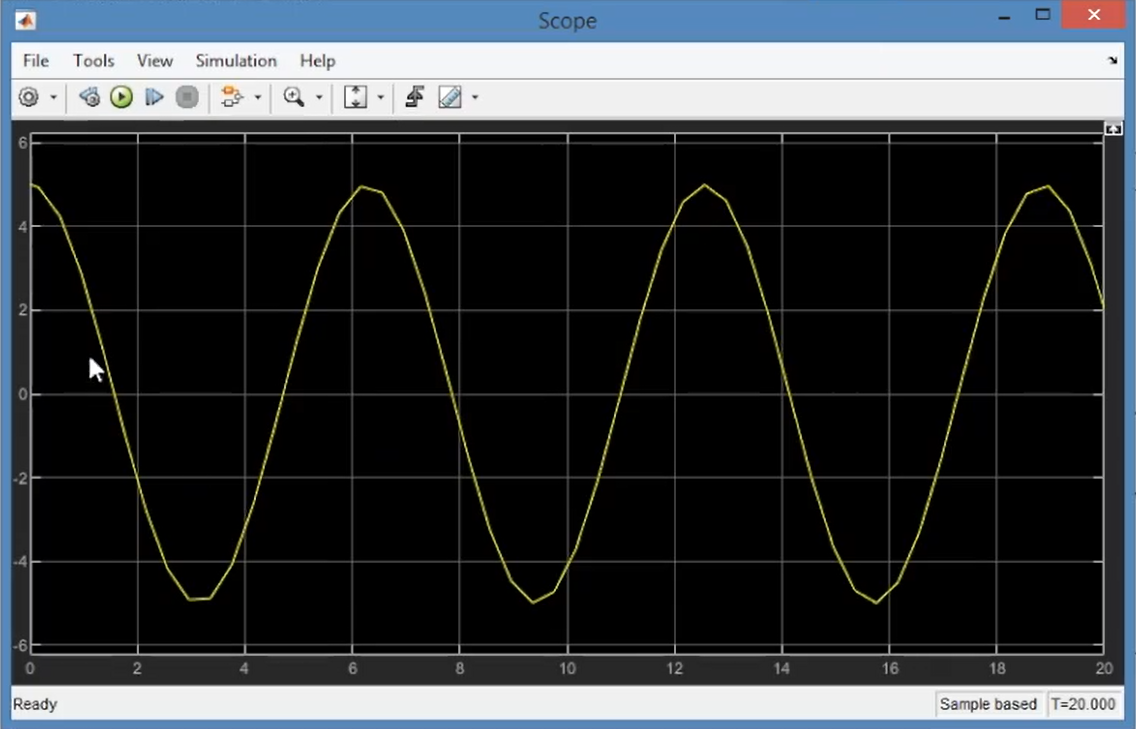
- $-1<\zeta<0$,这种情况就直接发散了。
一、跟踪一条直线
仍统一使用之前的符号说明,假设$\eta$角很小,这在航路飞行中的大部分时间都是满足的。
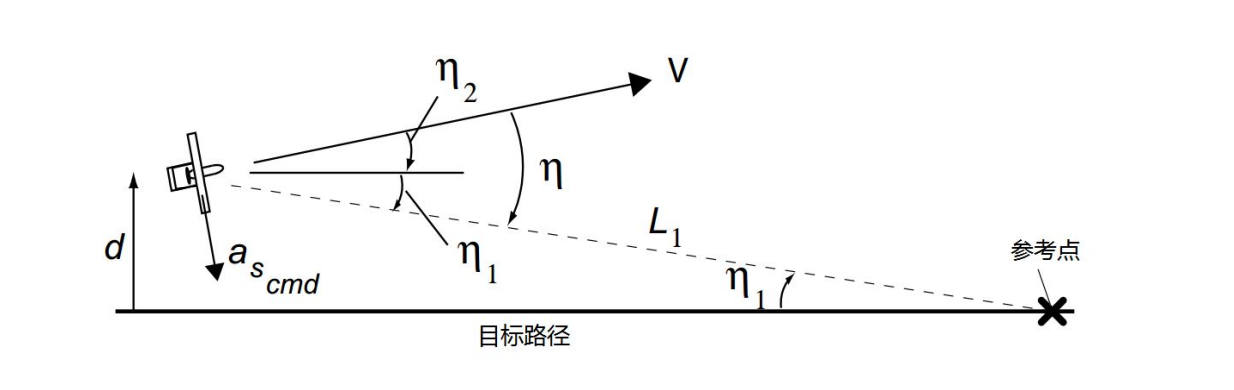
由于$\eta$很小,所以:
而且由于$\eta_1$和$\eta_2$很小,所以有:
综合上面有:
可以看到通过线性化之后,直线路径跟踪的L1制导律可以近似为一个PD控制器,来控制航迹误差。我们假设不考虑内环动力学,如不考虑内环滚转角控制器通过滚转角产生横向加速度的动力学延迟等,我们认为横向加速度是瞬间产生的,同时假设了$\eta_2$很小,则有:
进而可写成到:
其中$\zeta = \frac{1}{\sqrt{2}}\approx0.707$,$\omega_n=\frac{\sqrt{2}V}{L_1}$,这表明直线跟踪情况可近似看作一个简单二阶系统。
二、跟踪一条圆形路径
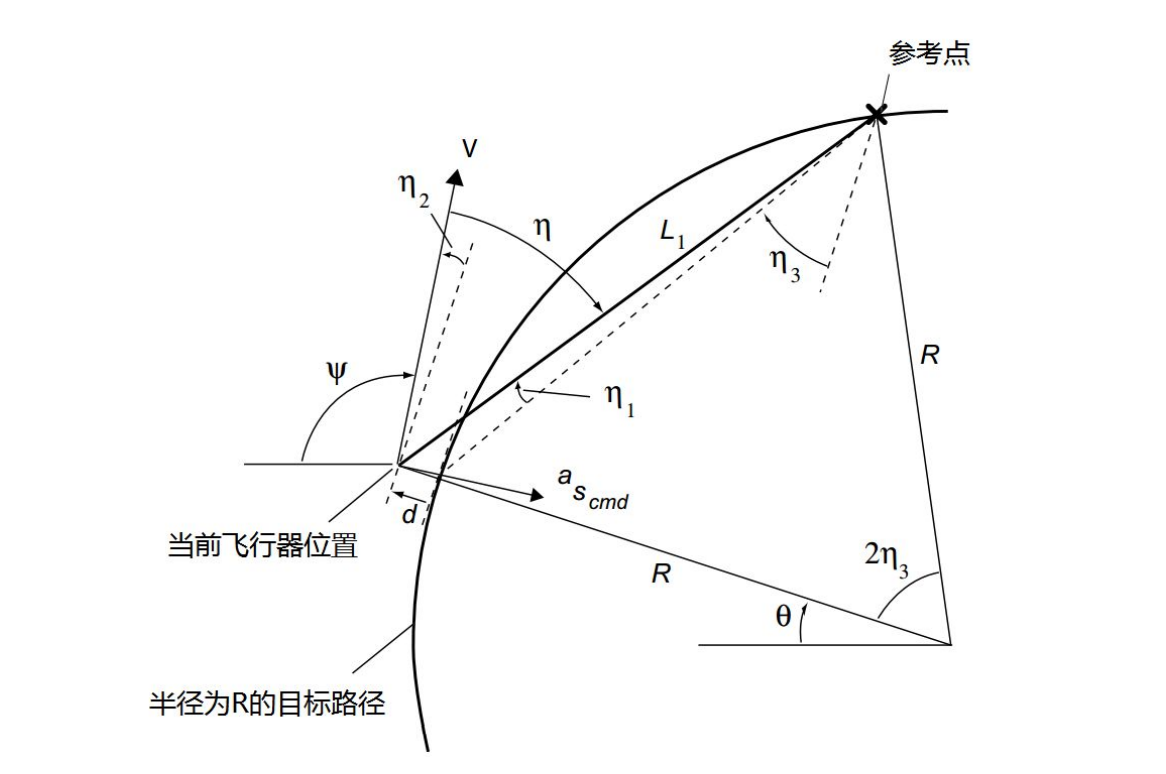
圆弧路径跟踪情况如上图,假设$\eta_1$和$\eta_2$都很小,飞行器的当前位置取决于R+d和$\theta$,而$\psi$决定了飞行器当前速度矢量的方向。因为:
所以:
由于$\eta_1$比较小,d也比较小,所以有:
定义:
基于上面小角度假设,位置误差的变化率就可表示为:
则:
因此横向加速度可表示为:
在$\eta_1$和$\eta_2$都很小的假设下:
以上是以速度V绕半径R的圆所需要的向心加速度,则:
在$\eta_1$和$\eta_2$都很小的假设下
其中:
于是化简可得:
于是又可得到:
其中:
可以看到,跟踪圆的情况也可以近似看成是一个简单二阶系统。
PX4中关于该算法的改进
从上面的分析可以看出,L1制导算法可以看成一个典型的二阶系统,阻尼比是固定的0.707,自然频率$\omega_n$正比于飞行器速度与L1的比值,也就是说,如果L1是固定的,那么这个二阶系统的自然频率是随着飞行速度变化而变化的,这就不能保证飞机在任何速度下都能有良好的跟踪性能,所以px4中L1和V的比值是固定的,这样就可以保证系统的自然频率是固定的。
同理,上面的计算也可以看出系统的阻尼比$\zeta$也是固定的,为0.707,但是实际飞行时,切向加速度达到期望值存在响应延迟时间,融合速度反馈也存在延迟,因此系统的阻尼比应可以调节,以满足考虑内环动力学系统之后整体系统阻尼比的要求。
PX4中,调节L1控制系统阻尼比的参数为FW_L1_DAMPING,调节自然频率的参数为FW_L1_PERIOD,其实实际调试好系统姿态环参数之后,关于L1调试的参数重要的只有这两个参数,且这两个参数调节起来也异常简单。那么如何实现阻尼比和自然频率的修改呢,通过修改加速度增益参数即可。以直线跟踪为例:
上面的推导中我们得到:
增加加速度增益后,期望的横向加速度表示为:
又有:
所以系统微分方程可写成如下形式:
对照二阶系统微分方程格式:
有:
这样我们通过FW_L1_DAMPING参数设置了$\zeta$,即$\zeta$=FW_L1_DAMPING,程序中会自动计算出K来,其中 $\omega_n = \sqrt{K}\frac{V}{L_1}$,所以有:
同理我们通过FW_L1_PERIOD可以设置系统的自然周期,也就间接设定了系统的自然频率,注意到FW_L1_PERIOD的单位是s,所以:
我们之前已经通过参数确定了阻尼比$\zeta$,进而K也确定了,现在我们也确定了自然频率$\omega_n$,那么就可以通过当前速度计算出当前L1制导中使用的L1线段长度:
这样处理之后就可以保证达到我们想要的系统阻尼比和自然频率了。PX4中该部分处理如下:
1 | void ECL_L1_Pos_Controller::set_l1_period(float period) |
求L1长度:
1 | /* calculate the L1 length required for the desired period */ |
求期望的切向加速度:
1 | _lateral_accel = _K_L1 * ground_speed * ground_speed / _L1_distance * sinf(eta); |
以直线航点跟踪跟踪为例,px4代码中的跟踪逻辑为:



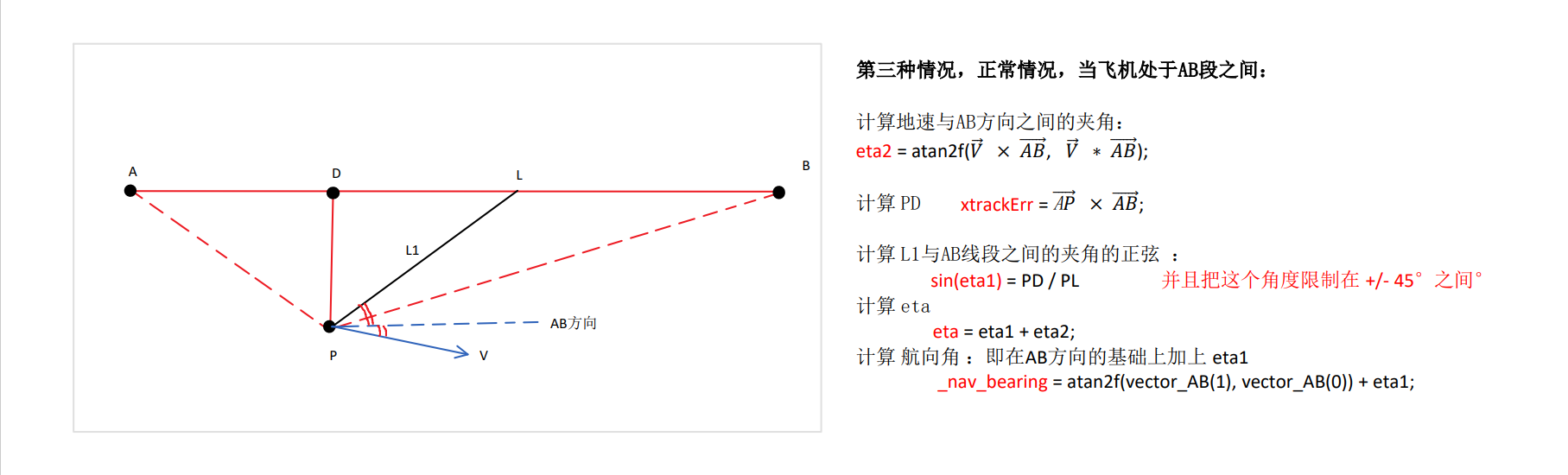

仿真
gazebo仿真下可以观察不同的FW_L1_PERIOD参数和FW_L1_DAMPING参数在飞行器拐入航线时的情况。
一、FW_L1_PERIOD不变
1、FW_L1_DAMPING = 0.75,= FW_L1_PERIOD = 12

2、FW_L1_DAMPING = 0.3, FW_L1_PERIOD = 12
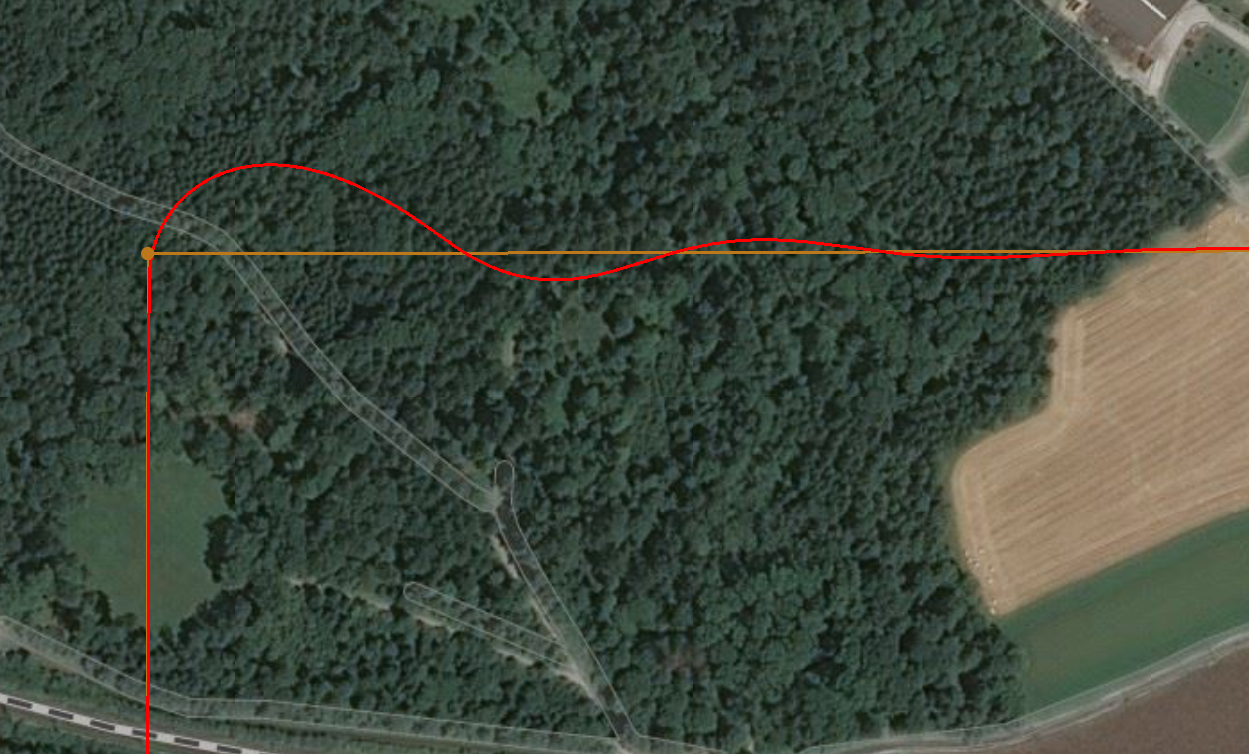
3、FW_L1_DAMPING = 1.2,FW_L1_PERIOD = 12

二、固定FW_L1_DAMPING不变
FW_L1_DAMPING = 0.3, FW_L1_PERIOD = 12
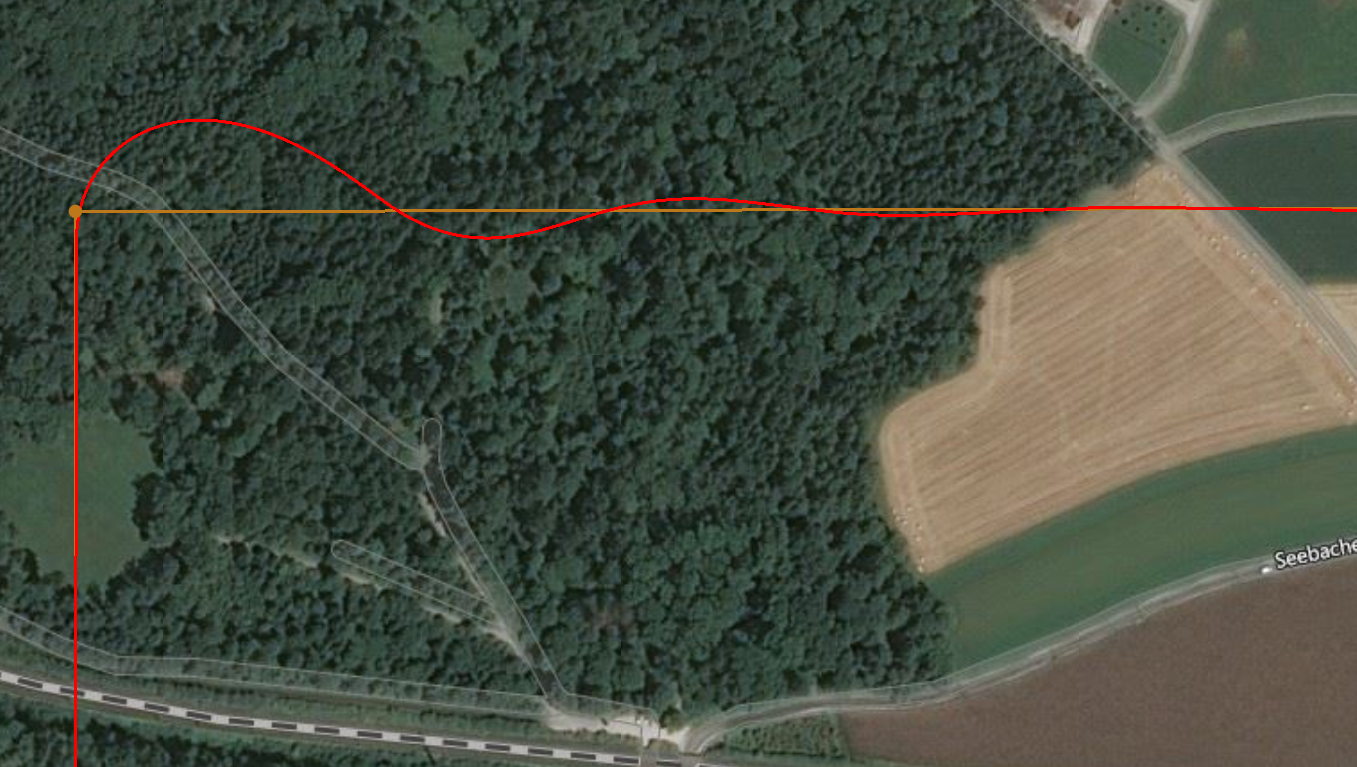
FW_L1_DAMPING = 0.3,= FW_L1_PERIOD = 3
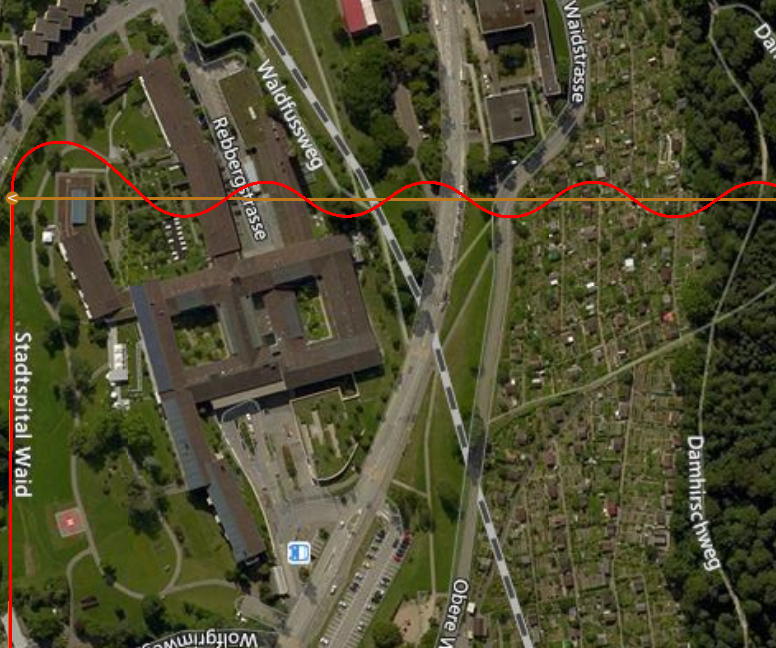
FW_L1_DAMPING = 0.3,=FW_L1_PERIOD = 50
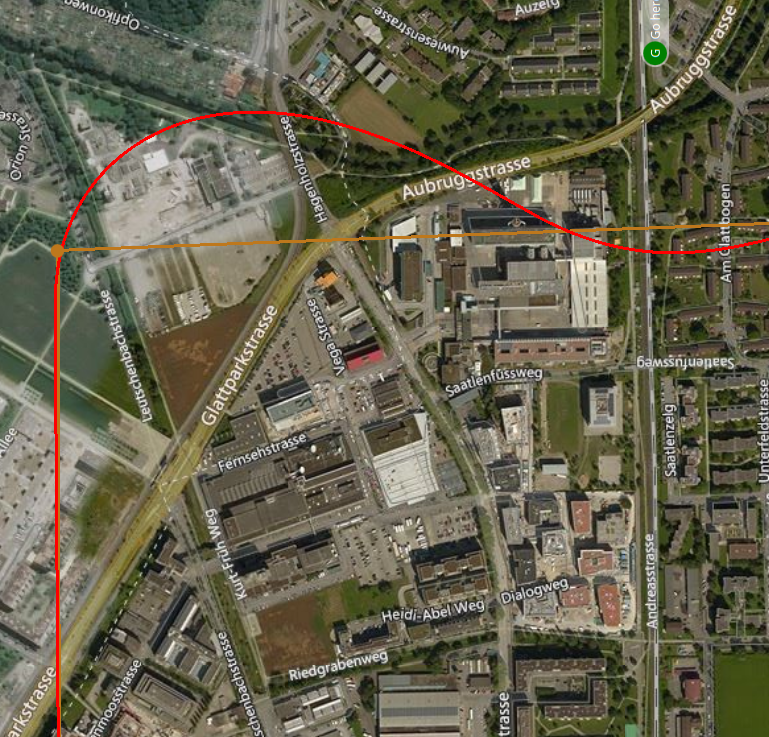
放在同一张图下看: