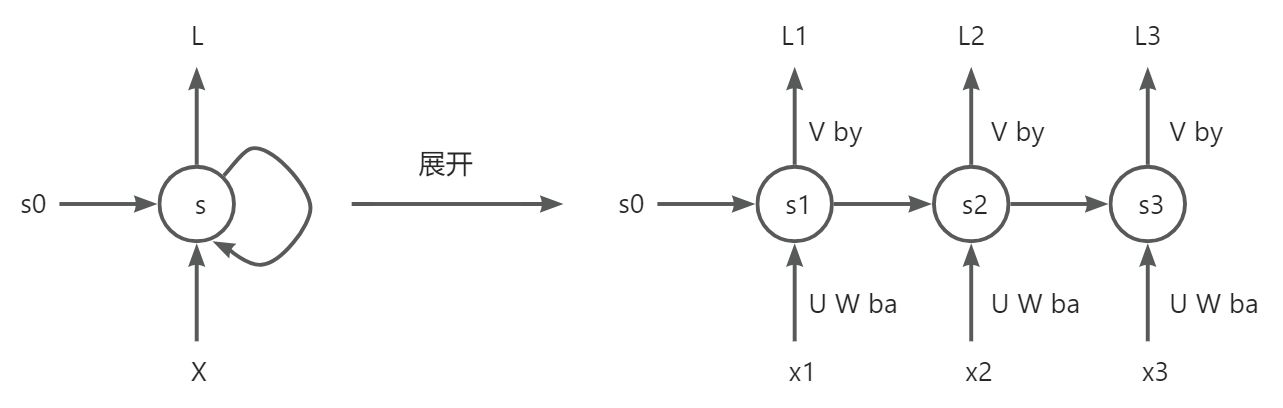
RNN前向传播与反向传播

前向传播

1. 第一层
   1. $ S_1 = tanh(Ux_1+WS_0+b_a) $
   2. $ y_1 = softmax(VS_1+b_y) $
   3. $ L_1 = L(y_1) $
2. 第二层
   1. $ S_2 = tanh(Ux_2+WS_1+b_a) $
   2. $ y_2 = softmax(VS_2+b_y) $
   3. $ L_2 = L(y_2) $
3. 第三层
   1. $ S_3 = tanh(Ux_3+WS_2+b_a) $
   2. $ y_3 = softmax(VS_3+b_y) $
   3. $ L_3 = L(y_3) $
4. 对于最终的损失函数，是每一层的损失函数相加即：
   1. $ L = L_1 + L_2 + L_3 $
5. 注：U V W ba by参数是共享的

反向传播

1. 第三层

   1. $\begin{cases} \frac{\partial L}{\partial V} = \frac{\partial L}{\partial L_3} \frac{\partial L_3}{\partial y_3} \frac{\partial y_3}{\partial V} \\ \frac{\partial L}{\partial b_y} = \frac{\partial L}{\partial L_3} \frac{\partial L_3}{\partial y_3} \frac{\partial y_3}{\partial b_y} \end{cases}$
   2. $ \frac{\partial L}{\partial S_3} = \frac{\partial L}{\partial L_3} \frac{\partial L_3}{\partial y_3} \frac{\partial y_3}{\partial S_3} $
   3. $\begin{cases} \frac{\partial L}{\partial U} = \frac{\partial L}{\partial S_3} \frac{\partial S_3}{\partial U} \\
      \frac{\partial L}{\partial W} = \frac{\partial L}{\partial S_3} \frac{\partial S_3}{\partial W} \\
      \frac{\partial L}{\partial b_a} = \frac{\partial L}{\partial S_3} \frac{\partial S_3}{\partial b_a} \end{cases} $

2. 第二层

   1. $\begin{cases} \frac{\partial L}{\partial V} = \frac{\partial L}{\partial L_2} \frac{\partial L_2}{\partial y_2} \frac{\partial y_2}{\partial V} \\
      \frac{\partial L}{\partial b_y} = \frac{\partial L}{\partial L_2} \frac{\partial L_2}{\partial y_2} \frac{\partial y_2}{\partial b_y} \end{cases}$

   2. 对$ S_2 $的求导有些不同，因为它有2条路径可以到达损失函数

      $$\begin{aligned} & S_2 \to y_2 \to L_2 \to L\\ & \downarrow \\ & S_3 \to y_3 \to L_3 \to L \end{aligned}$$

      因此，对$ S_2 $​的求导为：

      $$\frac{\partial L}{\partial S_2} = \frac{\partial L}{\partial L_2} \frac{\partial L_2}{\partial y_2} \frac{\partial y_2}{\partial S_2} + \frac{\partial L}{\partial L_3} \frac{\partial L_3}{\partial y_3} \frac{\partial y_3}{\partial S_3} \frac{\partial S_3}{\partial S_2} \\ =\frac{\partial L}{\partial L_2} \frac{\partial L_2}{\partial y_2} \frac{\partial y_2}{\partial S_2} + \frac{\partial L}{\partial S_3} \frac{\partial S_3}{\partial S_2}$$

   3. $ \begin{cases}
      \frac{\partial L}{\partial U} = \frac{\partial L}{\partial S_2} \frac{\partial S_2}{\partial U} \\
      \frac{\partial L}{\partial W} = \frac{\partial L}{\partial S_2} \frac{\partial S_2}{\partial W} \\
      \frac{\partial L}{\partial b_a} = \frac{\partial L}{\partial S_2} \frac{\partial S_2}{\partial b_a}
      \end{cases}$

3. 第一层

   1. $ \begin{cases}
      \frac{\partial L}{\partial V} = \frac{\partial L}{\partial L_1} \frac{\partial L_1}{\partial y_1} \frac{\partial y_1}{\partial V} \
      \frac{\partial L}{\partial b_y} = \frac{\partial L}{\partial L_1} \frac{\partial L_1}{\partial y_1} \frac{\partial y_1}{\partial b_y}
      \end{cases} $

   2. 对$ S_1 $的求导有些不同，因为它有3条路径可以到达损失函数: $\begin{aligned} & S_1 \to y_1 \to L_1 \to L \\ & \downarrow \\ & S_2 \to y_2 \to L_2 \to L \\ & \downarrow \\ & S_3 \to y_3 \to L_3 \to L \end{aligned}$ 因此对$ S_1 $的导数为:

      $$\frac{\partial L}{\partial S_1} = \frac{\partial L}{\partial L_1} \frac{\partial L_1}{\partial y_1} \frac{\partial y_1}{\partial S_1} + \frac{\partial L}{\partial L_2} \frac{\partial L_2}{\partial y_2} \frac{\partial y_2}{\partial S_2} \frac{\partial S_2}{\partial S_1} + \frac{\partial L}{\partial L_3} \frac{\partial L_3}{\partial y_3} \frac{\partial y_3}{\partial S_3} \frac{\partial S_3}{\partial S_2} \frac{\partial S_2}{\partial S_1} \\ = \frac{\partial L}{\partial L_1} \frac{\partial L_1}{\partial y_1} \frac{\partial y_1}{\partial S_1} + \frac{\partial S_2}{\partial S_1} (\frac{\partial L}{\partial L_2} \frac{\partial L_2}{\partial y_2} \frac{\partial y_2}{\partial S_2} + \frac{\partial L}{\partial L_3} \frac{\partial L_3}{\partial y_3} \frac{\partial y_3}{\partial S_3} \frac{\partial S_3}{\partial S_2} ) \\ = \frac{\partial L}{\partial L_1} \frac{\partial L_1}{\partial y_1} \frac{\partial y_1}{\partial S_1} + \frac{\partial S_2}{\partial S_1} (\frac{\partial L}{\partial L_2} \frac{\partial L_2}{\partial y_2} \frac{\partial y_2}{\partial S_2} + \frac{\partial L}{\partial S_3} \frac{\partial S_3}{\partial S_2} ) \\ = \frac{\partial L}{\partial L_1} \frac{\partial L_1}{\partial y_1} \frac{\partial y_1}{\partial S_1} + \frac{\partial S_2}{\partial S_1} (\frac{\partial L}{\partial S_2})$$

   3. 对另外3个参数的求导：

      $$\begin{cases} \frac{\partial L}{\partial U} = \frac{\partial L}{\partial S_1} \frac{\partial S_1}{\partial U} \\ \frac{\partial L}{\partial W} = \frac{\partial L}{\partial S_1} \frac{\partial S_1}{\partial W} \\ \frac{\partial L}{\partial b_a} = \frac{\partial L}{\partial S_1} \frac{\partial S_1}{\partial b_a} \end{cases}$$

简要总结

• 我们看到 U V W ba by参数是共享的，那我们为什么在计算最终更新用的梯度时需要将计算的每一层的 U V W ba by 的梯度相加呢？可以这么理解：
  • 最终的损失函数其实是每一层的损失函数求和的形式，如上述：$ L = L_1 + L_2 +L_3 $
  • 那么其实对于每一层，我们求每一层的损失函数相对于 U V W ba by 的梯度，这是如果要求 总的损失函数L 相对于 U V W ba by 的梯度，直接将每一层的损失函数求出的相对于U V W ba by 的梯度相加即可
  • 由于总的函数相对于每一层的损失函数的导数都是1，所以我们可以直接将L相对于U V W ba by的梯度直接相加即可
  • 问题：如果我们更看重某一层的输出，比如最后一层的输出，是不是可以将最后一层的损失函数前乘以一个权重系数来使学习的结果在最后一层输出的更为准确一些，比如写成$ L = 0.1L_1 + 0.1 L_2 + 0.8 L_3 $
• 另一种理解：微分量线性叠加
  • 假设 U V W ba by均是一个数值，他们构成了一个 5维的线性空间
  • 每一层的 δU δV δW δba δby 都会对总的L产生 δL的变化
  • 每一层的 δU δV δW δba δby可以看成一个线性空间的微小向量 [δU δV δW δba δby]
  • 那么所有层的影响即将每一个层的微小的向量加起来即可，这样就可以得到整个网络综合 U V W ba by在每一层的微小变化带来的对损失函数的影响

• 通用公式总结：

  1. $$\frac{\partial L}{\partial V} = \sum_{n=1}^3 \frac{\partial L}{\partial L_i} \frac{\partial L_i}{\partial y_i} \frac{\partial y_i}{\partial V} \\ \frac{\partial L}{\partial b_y} = \sum_{n=1}^3 \frac{\partial L}{\partial L_i} \frac{\partial L_i}{\partial y_i} \frac{\partial y_i}{\partial b_y}$$
  2. $$\frac{\partial L}{\partial S_i} = =\frac{\partial L}{\partial L_i} \frac{\partial L_i}{\partial y_i} \frac{\partial y_i}{\partial S_i} + \frac{\partial L}{\partial S_{i+1}} \frac{\partial S_{i+1}}{\partial S_i}$$
  3. $$\frac{\partial L}{\partial U} = \sum_{n=1}^3 \frac{\partial L}{\partial S_i} \frac{\partial S_i}{\partial U} \\ \frac{\partial L}{\partial W} = \sum_{n=1}^3 \frac{\partial L}{\partial S_i} \frac{\partial S_i}{\partial W} \\ \frac{\partial L}{\partial b_a} = \sum_{n=1}^3 \frac{\partial L}{\partial S_i} \frac{\partial S_i}{\partial b_a}$$

• 梯度消失和梯度爆炸

  1. 说明：我理解的梯度消失可能和以前我认为的不一样，因为从上面的公式总结来看，即使存在梯度累乘的情况，比如：对于第一层的W， $\frac {\partial S_i}{\partial W}$可以写为$\frac{\partial S_i}{\partial W} = \frac{\partial S_i}{\partial S_{i-1}} \frac{\partial S_{i-1}}{\partial S_{i-2}} \frac{\partial S_{i-2}}{\partial S_{i-3}} ... \frac{\partial S_2}{\partial S_1} \frac{\partial S_1}{\partial W}$但这只是整个K层网络求 $\frac{\partial L}{\partial W} = \sum_{n=1}^K \frac{\partial L}{\partial S_i} \frac{\partial S_i}{\partial W} \\$ 累加的一个项，靠后的网络仍然还是能够计算出梯度的，只是靠前的久远的网络无法对梯度更新作出贡献了，并不代表 U V W ba by不能更新（记住，这些参数是共享的），只是最后学习出来，网络可能只学习了后面几层的时序关系，也即无法捕获时序序列较久远（靠前）的信息而已，但并不会导致最优化求解失败。
  2. 梯度爆炸：因为每一层都对 U V W ba by有贡献，那么如果通过累乘传递到较前的网络就直接导致较前网络计算出的梯度变大，同时由于每一层都会对 U V W ba by有贡献，极端情况下，如果前面层的贡献已经无穷大了，那么整个网络在学习时更新 U V W ba by就会失败。

Reference

1. https://zhuanlan.zhihu.com/p/31842423
2. https://zhuanlan.zhihu.com/p/44163528
3. https://link.zhihu.com/?target=http%3A//proceedings.mlr.press/v28/pascanu13.pdf

赏

谢谢你请我吃糖果

支付宝

微信