注:从ResNet论文逻辑来看,将AI看作是一门实验学科或许更容易使人接收AI的一些结果,至于可解释性,则需要在实验中不断发展完善,这两者并不冲突,就像物理学科的发展也是实验理论相辅相成。
1. Background
Deep learning models, particularly convolutional neural networks (CNNs) have achieved remarkable success in image-related tasks. However, training very deep networks (e.g. networks with hundreds of layers) faced a critical challenge: the vanishing gradient or exploding gradient problem. As networks became deeper, gradients during back propagation diminished or exploded, making it difficult to train the network effectively.
2. Introduction
To address this challenge, He et al. proposed ResNet in 2015. The paper introduced the concept of residual learning, which allowed the training of extremely deep networks by explicitly reformulating the learning process. ResNet not only won the ILSVRC classification competition but also became a cornerstone for subsequent deep learning research. Its core innovation is the residual block, which employs skip connections (or shortcuts) to enable direct propagation of input signals across layers. By learning residual mappings (differences from the input) instead of complete transformations, ResNet mitigates vanishing gradients and simplifies optimization for extremely deep models (e.g. ResNet-50, 101, 152).
3. Methods
ResNet introduced the concept of residual blocks, which enable the training of extremely deep networks by learning residual functions instead of the original mappings. The key innovation is the introduction of skip connections (or residual connections), which allow the gradient to flow through the network more effectively.
Architecture Details:
- Residual Blocks: Each residual block consists of two or three convolutional layers. The input is added to the output of the block, forming a residual connection.
- Identity Mapping: The residual block ensures that the output of the block can directly learn the identity function, which simplifies optimization.
- Network Depth: ResNet demonstrated that deeper networks (e.g. 50, 101 or 152 layers) achieve better performance than shallow networks.
Key Equation:
The residual block can be defined as:
$ y = F(x, {W_i}) + x $
where (F) represents the transformations applied to the input (x).
4. Analysis of ResNet
Detailed Analysis:
- 一个问题:模型越深,是不是表现越好呢?
- 仅从现实层面考虑
- 结论:模型深度在一定范围内,模型越深表现越好,这意味着:
- 在一定数据量的情况下,可以适当地学习到数据之间的关系,而又不至于过拟合
- 原因如下:
- 模型深度过深,表现不一定越好(但不是说一定会差)
- 假设训练数据就是 $ y = ax + b $这条曲线生成的数据,我们不添加任何噪声,那么我们假设两个模型,分别是:
- Model1:$ y=wx + b_1 $
- Model2:$ y = w_1x^2 + w_2x+b_2 $
- 假设选取这条曲线生成的数据的一部分,来训练这两个模型的参数,另一部分数据用于测试。显然,Model1训练好之后,最优情况为$ w = a, b_1 = b $并能在测试数据表现出100%的正确率。对于Model2,最好的训练情况是参数$ w_1 $训练结果为0,而$ w_2 = a, b_2 = b $,此时其表现和Model1是一致的,但是任何其他训练出的参数,其表现将会比Model1差。从这个方面我们认为,并不是模型越深,表现就越好,而是和模型所要解决的问题有关。
- 假设训练数据就是 $ y = ax + b $这条曲线生成的数据,我们不添加任何噪声,那么我们假设两个模型,分别是:
- 所以个人认为,增大模型的深度取决于我们所要解决的问题,每一个问题或者任务都有其模型深度上限,在到达此上限之前,通过增大模型深度,能够提高模型的表现,但是一旦超过这个上限,模型的最优表现虽然不会上升,但至少不会变差。但实际情况下,我们往往很难找到模型的最优解,这意味着模型的表现会下降。那么,我们能不能使模型的表现至少不会下降呢?ResNet的最大贡献就在此处,ResNet在很大程度上优化了这个问题。
- 模型表现的好坏和训练数据也有关系(这个其实和模型本身结构无关了,属于外部因素影响)
- 训练数据不可避免是存在噪声的,最极端的假设:假设训练数据接近无限,假设模型参数无限,那么可能得结果就是模型学习的过于全面,以至于将训练数据噪声之间的关系也全部学习了,此时模型的表现就不一定是最好的。
- 模型深度过深,表现不一定越好(但不是说一定会差)
- 结论:模型深度在一定范围内,模型越深表现越好,这意味着:
- 仅从现实层面考虑
另一种理解
- 问题:神经网络深度很重要,但是越深越难训练,因为网络堆叠加深会导致梯度消失或者梯度爆炸,导致在一开始就影响网络的学习收敛。这个问题很大程度可以有标准初始化和中间标准化层来解决。此时一个新问题出现了,在我们解决了梯度消失和梯度爆炸问题后,随着网络深度的增加,网络的精度达到了饱和(这个在预料之中,网络肯定有精度上限的),但,之后精度迅速下降,即学习退化问题出现了。且这种degradation并不是由overfitting导致的。
- 发现与假设:作者发现,随着网络深度增加,精度达到饱和(这点不奇怪),然后迅速下降,这一点并不符合常理。如果存在某个K层的网络f是当前的最优网络,那么可以构造一个更深的网络,使其最后几层为该网络f第K层输出的恒等映射(Identity Mapping)就可以取得和f一致的精度;如果K还不是最佳层数,那么更深的网络就可以取得更好的结果。总之,与浅层网络相比,更深的网络的表现不应该更差。因此一个合理的猜测就是:对神经网络来说,恒等映射并不容易拟合。因此作者提出了 residual learning framework
- 方法:即然如此,恒等映射不需要网络来学习了,直接通过shortcut connection引入恒等映射,网络学习除恒等映射之外的部分即可。
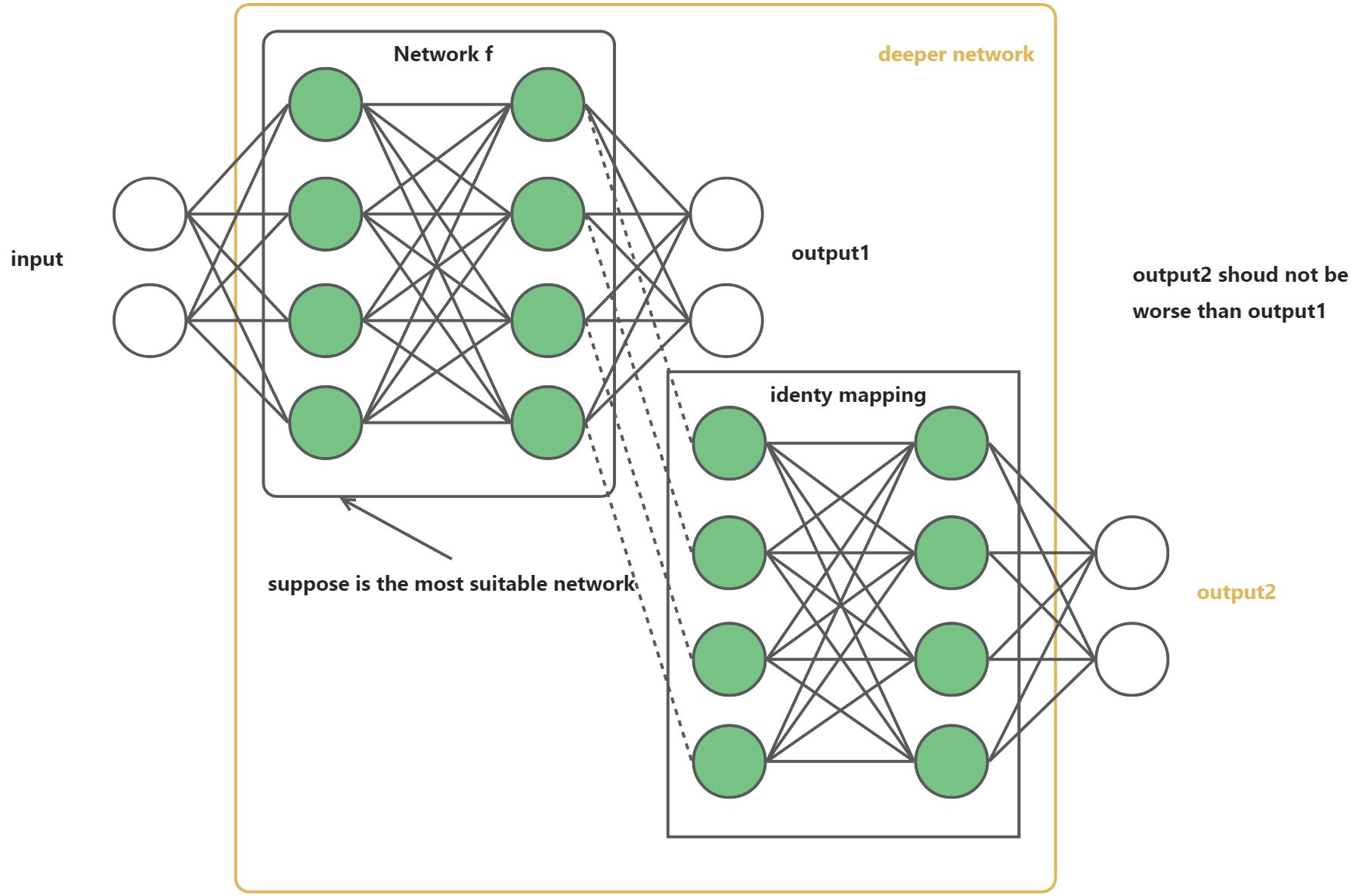
ResNet在解决什么问题?
- 网络“退化”问题,即更深的网络比更浅的网络表现更差
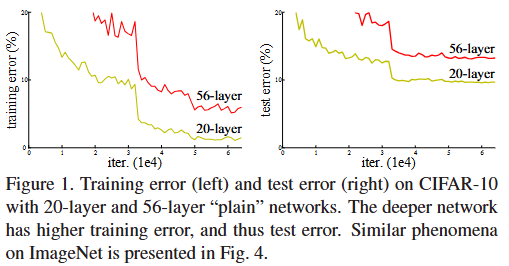
- 作者认为这种现象并不是overfitting导致的,而是网络退化(degradation),因为更深的网络不止test error更高,training error也更高。这意味着在训练更深的网络的时候出现了问题,当前的优化方法并没有求解出网络的最优解,导致出现较高的训练误差,这也必然导致在测试集上出现较高误差。这里面的原因如下:
- 随着网络的加深,梯度消失或梯度爆炸问题不可避免的出现,使得利用梯度下降之类的优化方法性能变差。当然Batch Normalization技术一定程度上极大缓解了此类问题,所以作者认为并不是梯度消失或者梯度爆炸导致了此问题。
- 对于非凸的非线性优化问题本身就很难求得全局最优解,面对更深的网络时,目前的优化算法存在瓶颈。
- ResNet作者提出了一种“残差连接”的网络结构,很大程度上缓解了上述问题:
- 作者在文章中提到:Let us consider a shallower architecture and its deeper counterpart that adds more layers onto it. There exists a solution by construction to the deeper model: the added layers are identity mapping, and the other layers are copied from the learned shallower model. The existence of this constructed solution indicates that a deeper model should produce no higher training error than its shallower counterpart. 且作者也在文章中说了,当前实验结果表明,相比于增加“残差连接”后优化的网络结构,在改变之前网络结构的情况下,目前的非线性优化求解器并不能求解出更好的结果:But experiments show that our current solvers on hand are unable to find solutions that are comparably good or better than the constructed solution (or unable to do so in feasible time).
- 注:“退化”并非指网络结构本身“劣化”,而是描述性能随深度增加而下降的客观现象。
- 网络“退化”问题,即更深的网络比更浅的网络表现更差
- 残差连接
- 论文中残差连接结构图如下,图中最明显的就是右侧的跳跃连接
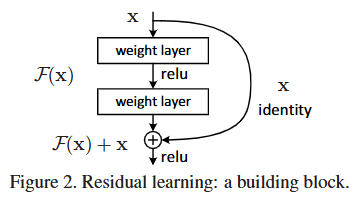
- 对残差连接的理解如下:
- 如论文中所说,这种连接带来的结果是网络最后学习的其实是$ F(x) $而不是$ F(x)+x $,其中$ F(x) $称之为残差。同时论文中写到:We hypothesize that it is easier to optimize the residual mapping than to optimize the original, unreferenced mapping. To the extreme, if an identity mapping were optimal, it would be easier to push the residual to zero than to fit an identity mapping by a stack of nonlinear layers.
- 上述假设暂时无证明,但可以尝试从以下几个方面来理解或者接收为啥ResNet可以表现更好
- 实验结果表明这样确实有效。作者说,这种残差形式是由退化问题激发的。根据前文,如果增加的层被构建为恒等映射(恒等函数),那么理论上,更深的模型的训练误差不应当大于浅层模型,但是出现的退化问题表明,求解器很难去利用多层网络拟合恒等映射(恒等函数)。但是,残差的表示形式使得多层网络近似起来要容易的多,如果恒等映射(恒等函数)可被优化近似,那么多层网络的权重就会简单地逼近0来实现恒等映射,即F(x) = 0。实验发现,学习到的残差函数通常响应值比较小,同等映射(shortcut)提供了合理的前提条件。所以,实验结果和假设相互印证。
- Shortcut connection 通过直接将输入数据(即较低层的特征)添加到输出数据上,使得梯度可以直接通过这一路径流动,从而缓解了梯度消失或爆炸的问题,进而缓解了求解模型参数的难度。即使网络深度加深,但求解器面对的问题变简单了,使用当前的求解器也能求解出更好的模型参数。
- 论文中残差连接结构图如下,图中最明显的就是右侧的跳跃连接
- 网络结构详解
- 整体架构如下
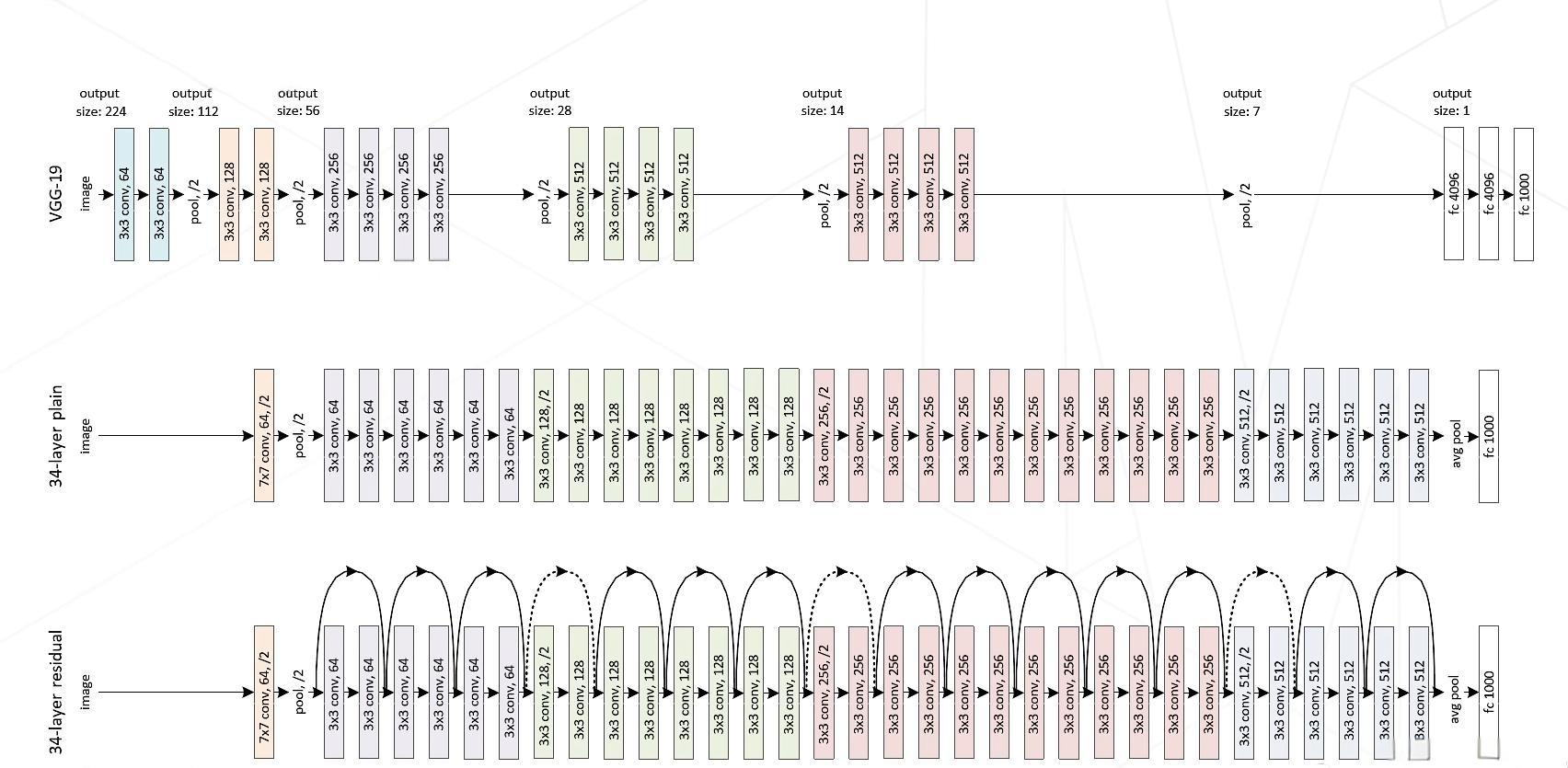
- 关于plain network设计的规则,论文中提到:
- For the same output feature map size, the layers have the same number of filters.
- If the feature map size is halved, the number of filters is doubled so as to preserve the time complexity per layer.
- 残差网络的设计是在plain network的基础上,增加shortcut connection,维度匹配的shortcut连接为实线,反之为虚线。对于维度不匹配的恒等映射,可以采用两种方法处理:
- The shortcut still performs identity mapping, with extra zero entries padded for increasing dimensions. This option introduces no extra parameter
- The projection shortcut is used to match dimensions (done by 1×1 convolutions). $ y = F(x, {Wi}) + W_sx. $即通过线性变换$ W_s $来实现维度匹配,不过这种方式会增加参数。
- 以34-layer residual network为例简单看一下维度的变化和设计规则的使用:
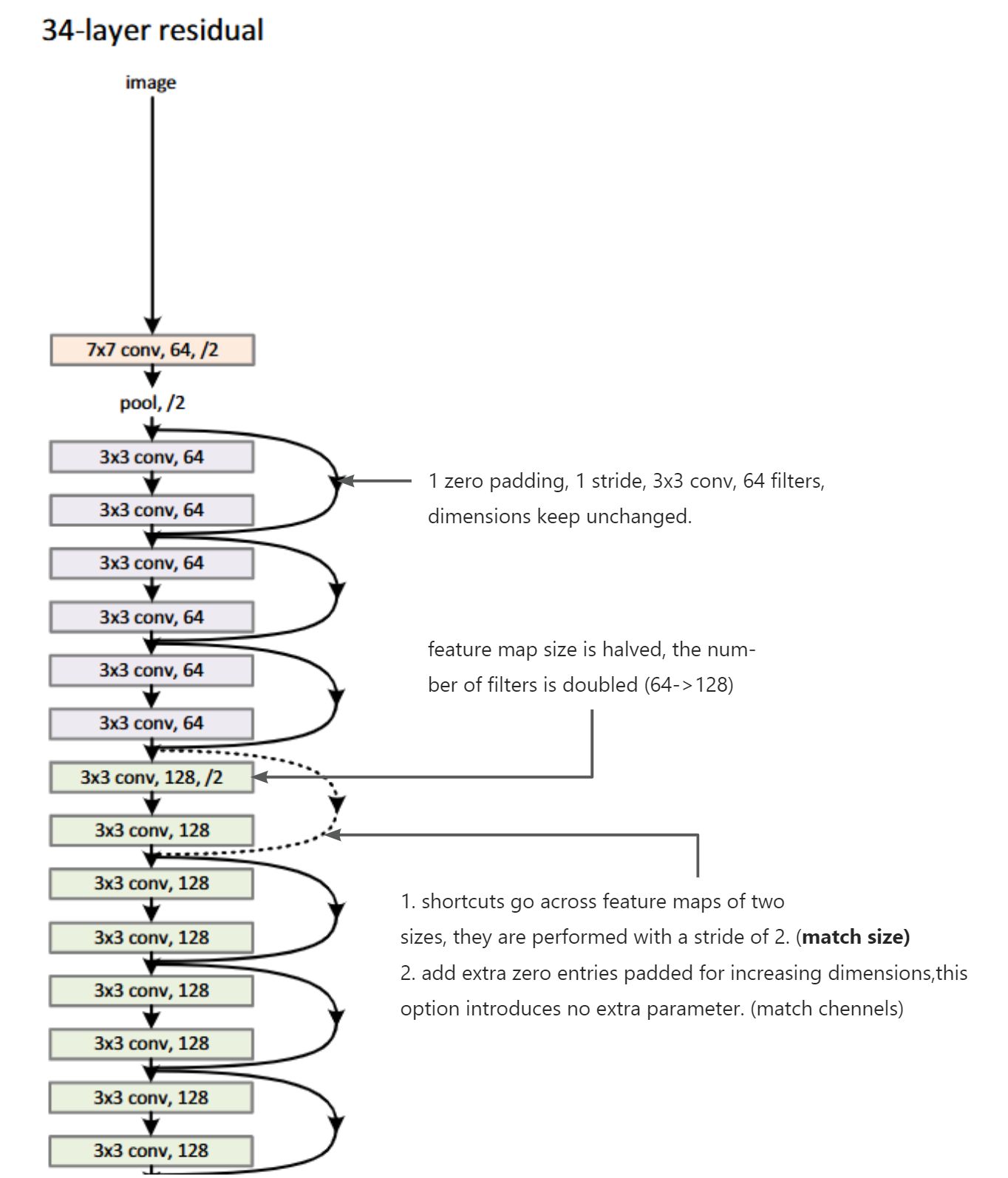
- 整体架构如下
Implementation
Key points
- Standard color augmentation.
- Adopt batch normalization (BN) right after each convolution and before activation.
- Use SGD with a mini-batch size of 256.
- Do not use dropout.
5. Experiments
ResNet was evaluated on the ILSVRC-2012 dataset, which contains 1.2 million high-resolution training images and 50,000 validation images. The experiments compared ResNet with other deep networks.
Plain Networks
论文作者 first evaluate 18-layer and 34-layer plain nets,观察到34-layer plain net has higher training error throughout the whole training procedure: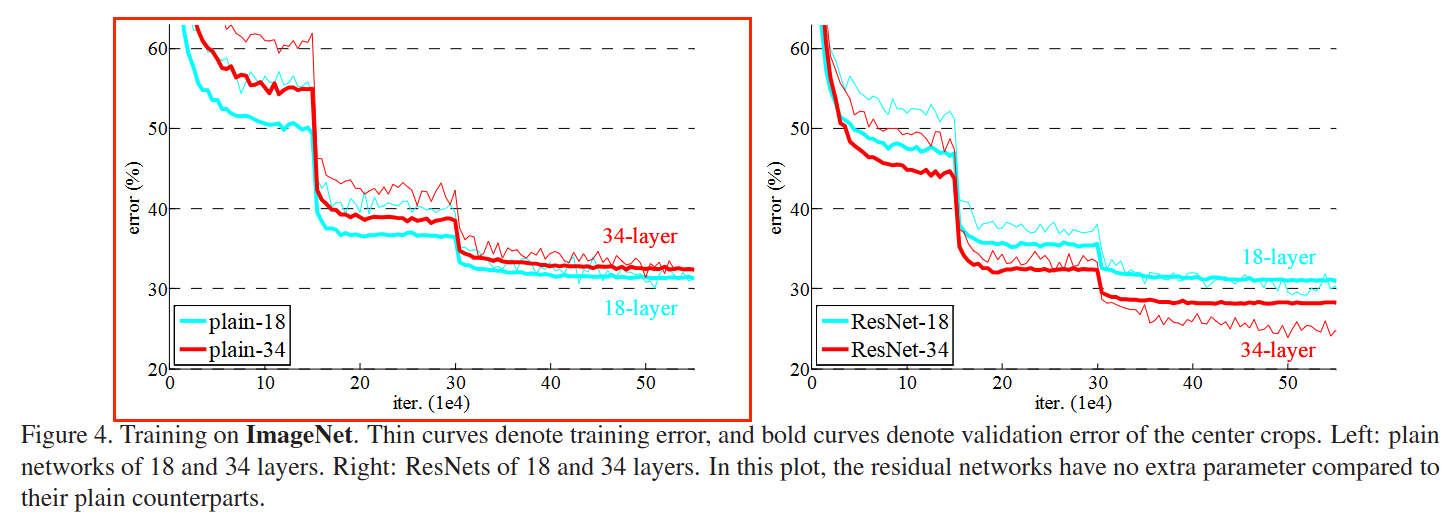
经过分析作者认为这个问题不是由于梯度消失或者梯度爆炸导致的,而是网络退化,原因如下:
- These plain networks are trained with BN, which ensures forward propagated signals to have non-zero variance.
- They also verify that the backward propagated gradients exhibit healthy norms with BN.
They conjecture that the deep plain nets may have exponentially low convergence rates, which impact the
reducing of the training error. The reason for such optimization difficulties will be studied in the future.
Residual Networks
作者评估了18-layer和34layer的ResNet,有三个重要观察:
- 34-layer ResNet is better than the 18-layer ResNet. This indicates that the degradation problem is well addressed in ResNet.
- ResNet reduces the top-1 error by 3.5% compared to its plain counterpart.This comparison verifies the effectiveness of residual learning on extremely deep systems. See Table 2.
- 18-layer plain/residual nets are comparably accurate (Table 2), but the 18-layer ResNet converges faster. This means that ResNet eases the optimization by providing faster convergence at the early stage.
| Table 2 | Plain | ResNet |
|---|---|---|
| 18 layers | 27.94 | 27.88 |
| 34 layers | 28.54 | 25.03 |
训练过程图如下图中右侧图: 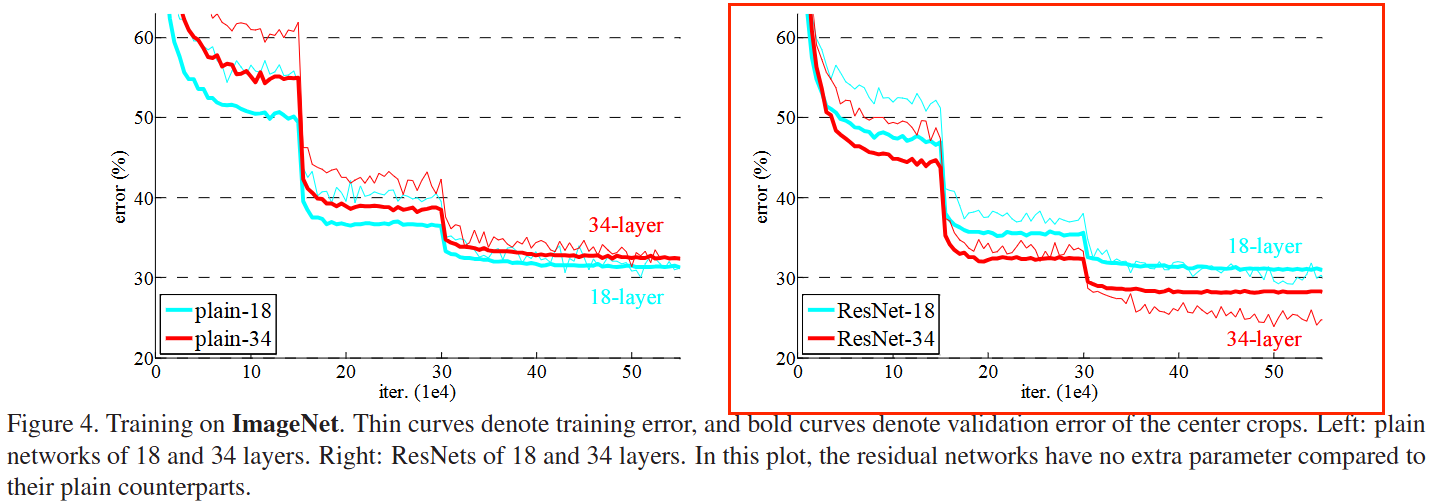
Extremely deep networks
Focusing on the behaviors of extremely deep networks, authors conducted more studies on the CIFAR-10 dataset. They tested deeper residual nets such as ResNet-50, ResNet-110, even ResNet-1202, got the following results: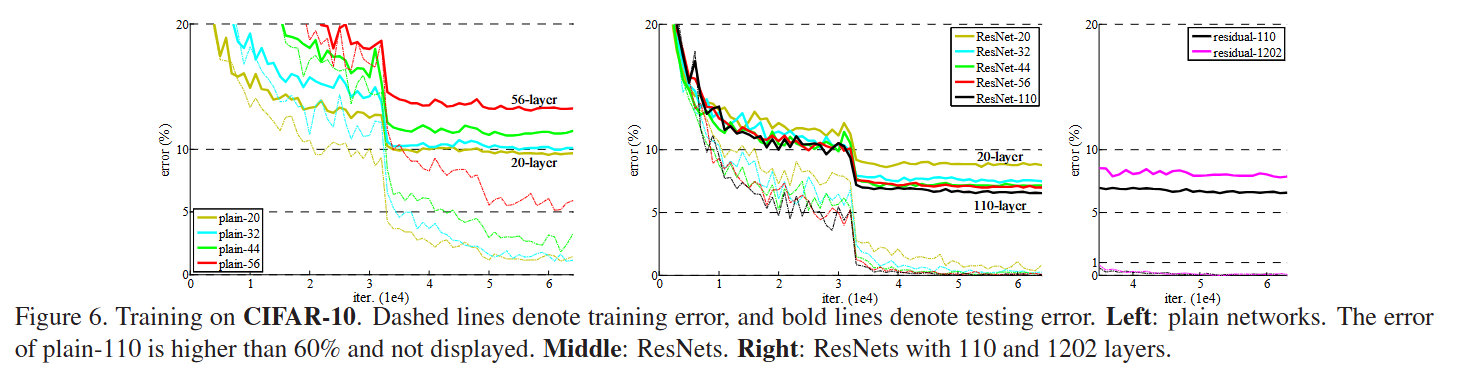
他们发现随着网络层数的加深,性能也在不断提升。作者最后在CIFAR-10上尝试了1202层的网络,结果在训练误差上与一个较浅的110层的相近,但是测试误差要比110层大1.5%,作者认为是采用了太深的网络,发生了过拟合。
另外,作者还分析了layer responses,得到下图:
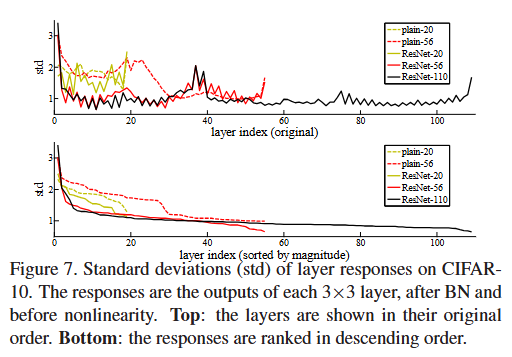
They think this figure shows that ResNets have generally smaller responses than their plain counterparts. These results support their basic motivation that the residual functions might be generally closer to zero than the non-residual functions.
Key Results:
- ResNet significantly outperformed previous state-of-the-art methods, demonstrating the effectiveness of residual learning.
6. Conclusion
Principles:
- ResNet introduces residual connections to simplify the learning of deep networks.
- The network learns the difference (residual) between the input and output, rather than the entire transformation.
Advantages:
- Enables the training of very deep networks (e.g. >100 layers).
- Improves model performance and generalization.
- Simple and computationally efficient.
Shortcomings:
- ResNet may not always benefit from increased depth, as very deep networks can sometimes perform worse than moderately deep ones.
- The model is primarily designed for image classification and may require modifications for other tasks.
7. References
- He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep Residual Learning for Image Recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR).
- Ren, S., He, K., Girshick, R., & Sun, J. (2015). Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. In IEEE Transactions on Pattern Analysis and Machine Intelligence.
- 关于resnet的ppt_mob6454cc7c0428的技术博客_51CTO博客


