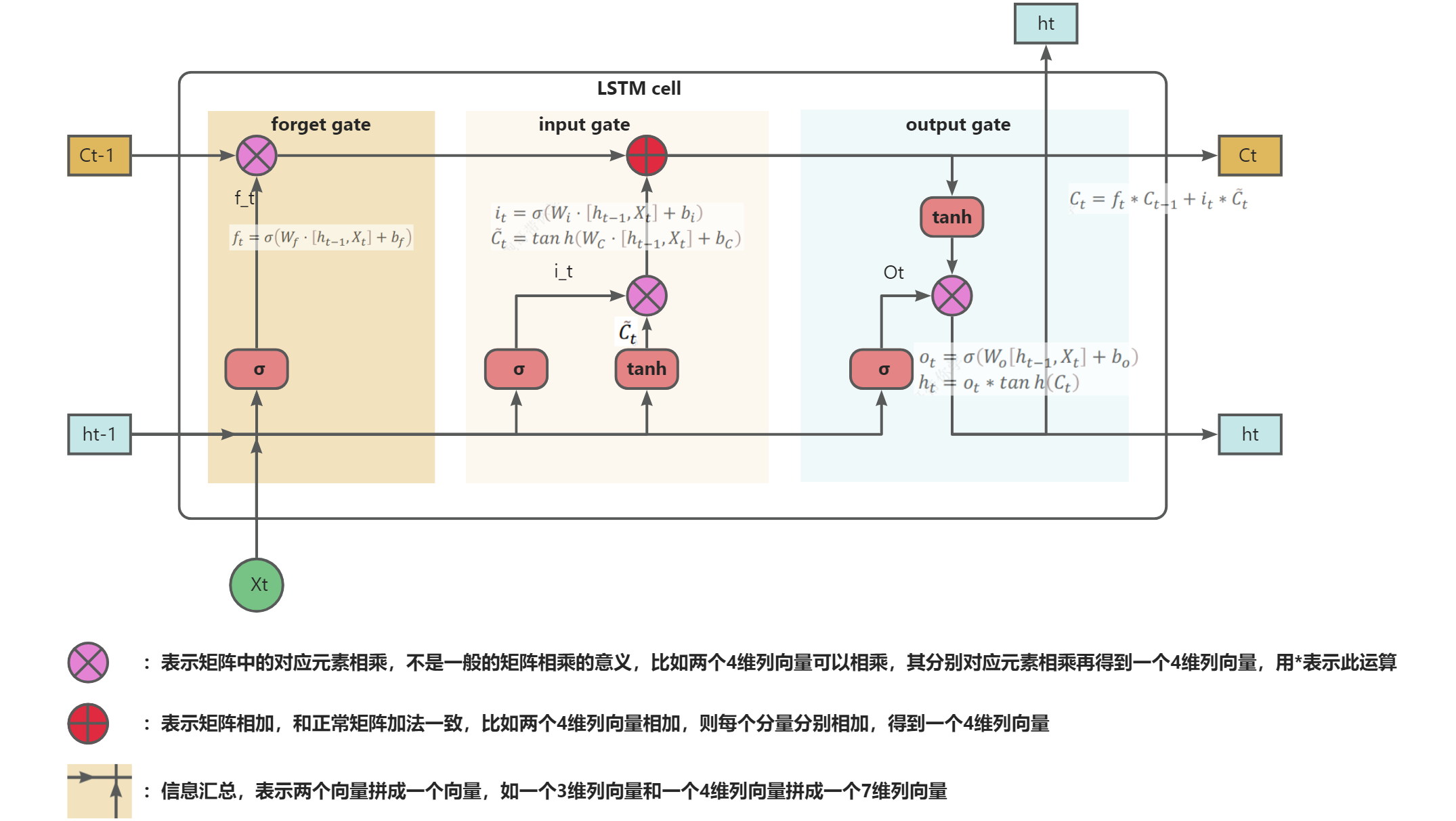
LSTM流程
如上图,假设在时刻t时刻,输入为, 前一时刻隐藏状态为,前一时刻细胞状态为,则LSTM的处理流程如下
1.遗忘门(forget gate)
遗忘门决定了我们应该从之前的细胞状态中遗忘哪些信息,公式为:
其中:
- $W_f$是遗忘门的权重矩阵
- $b_f$是遗忘门的偏置
- $\sigma$是$sigmoid$激活函数,该函数输出范围是(0,1),用于控制保留多少信息
- 矩阵计算示例图如下
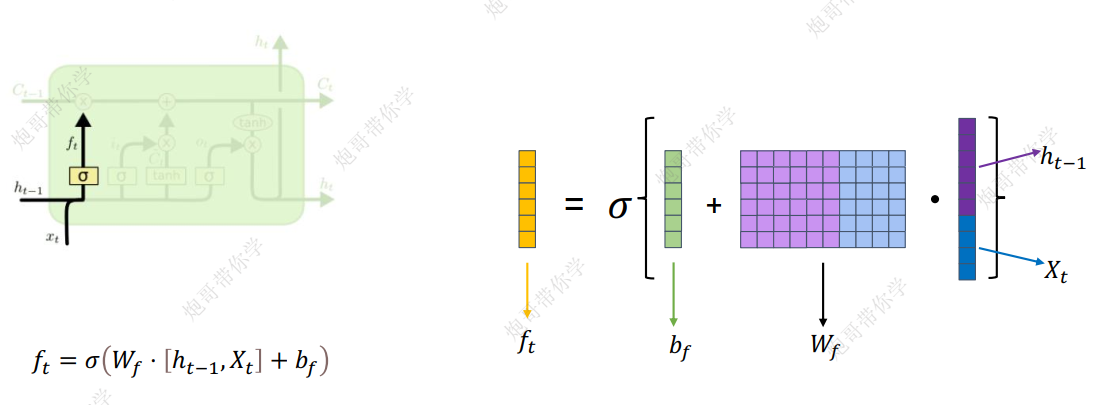
2.输入门(input gate)
输入门决定了有多少新的信息要加入到细胞状态$C_{t-1}$中,公式如下:
其中
- $i_t$将控制哪些新的信息加入细胞状态
- $\widetilde{C}_{t}$为计算出的新的信息,但最后哪些加入细胞状态是由上面的$i_t$控制的
- 计算示意图如下
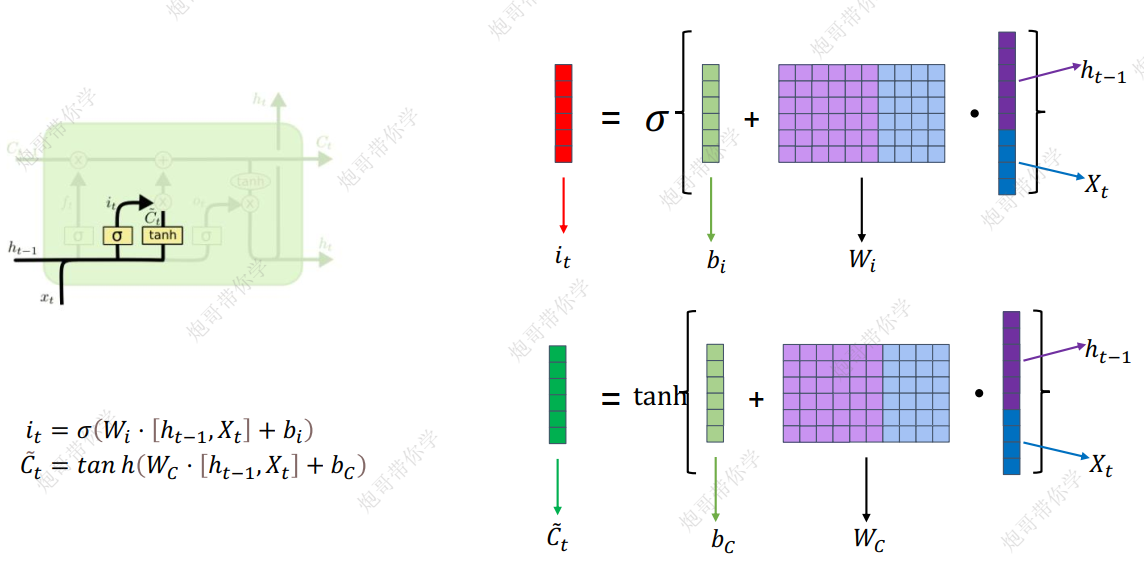
3.细胞状态更新
结合遗忘门和输入门的结果对细胞状态进行更新,这样记忆细胞可以抛弃一些无用的记忆,同时引入一些新的有用的记忆,公式如下
其中:
- 表示旧细胞中要保留的信息(虽说我们之前将第一道门称之为遗忘门,但其实选择旧细胞中的要保留的信息就是选择遗忘)
- 表示新加入到细胞中的信息
- 表示两个向量对应元素相乘再得到一个同维的向量(矩阵的哈达玛乘积),计算示意图如下
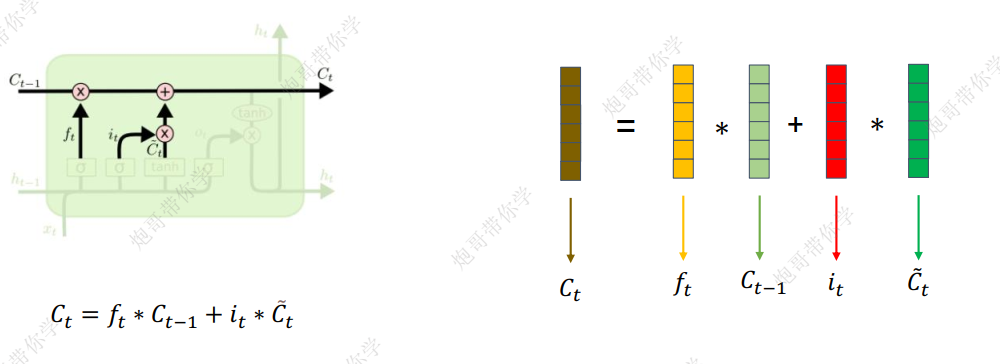
4.输出门(output gate)
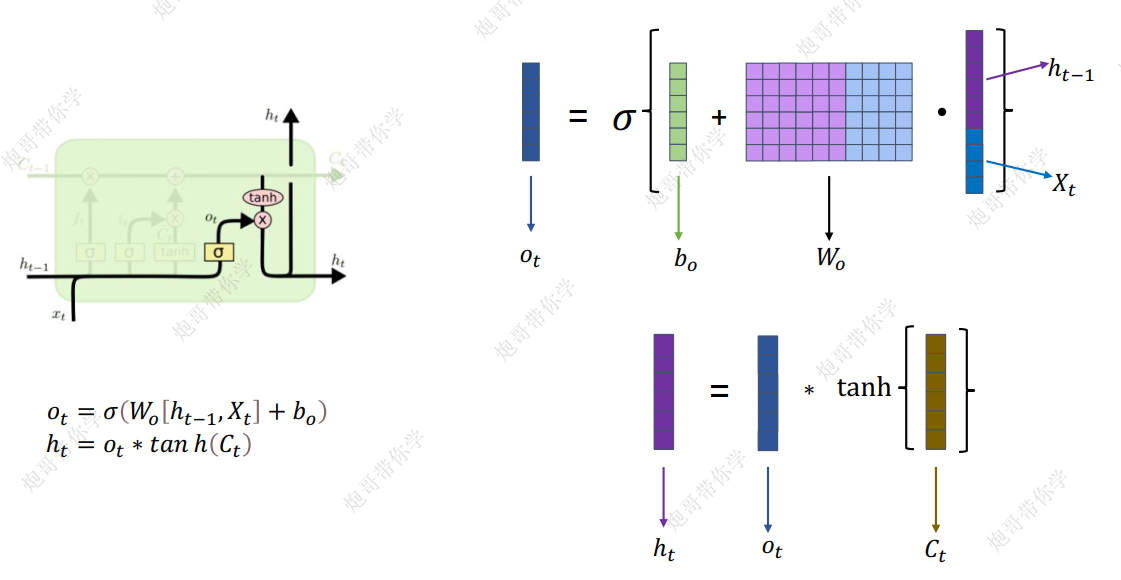
输出门决定了新的更新后的细胞中有哪些信息将被输出,作为当前时间步的隐藏状态,供下一时刻的细胞使用,公式为
其中
- $o_t$控制哪些更新后的细胞中的信息要输出
- 计算示意图如下
为何选用sigmoid和tanh
从我查阅的资料看,大致为以下原因:
- sigmoid函数的输出范围是(0, 1),它非常适合用于门控机制,因为门控需要一个介于0和1之间的值来表示“开启”或“关闭”的程度。在LSTM中,sigmoid用于遗忘门(Forget Gate)和输入门(Input Gate)的第一部分,以及输出门(Output Gate)。这些门控需要决定信息是否通过,sigmoid的输出恰好可以表示这种概率或比例。
- tanh函数的输出范围是(-1, 1),它适合用于表示一个值的范围或幅度,因为它可以输出负值和正值。在LSTM中,tanh用于初始化细胞状态的候选值(Candidate Values),以及最终的细胞状态和隐藏状态的计算。这些状态需要表示实际的值,而不仅仅是开启或关闭的比例,因此tanh可以提供更丰富的信息。
- sigmoid函数在接近0或1时梯度很小,这有助于避免梯度消失问题,尤其是在门控机制中。tanh函数在整个定义域内都有相对较大的梯度,这有助于在更新细胞状态时保持梯度的稳定性。
具体更深一步的原因需要再深入探索理解。
LSTM如何:缓解梯度消失
ref: Why LSTMs Stop Your Gradients From Vanishing: A View from the Backwards Pass (weberna.github.io)
- 解释1

- 解释2

- 注:上面的求导其实我还有很多疑问一时没有想通,先记录在此,如果大家看到,希望可以帮我解答一下
- 从向量维度来看, 并不是乘法运算,而是*哈达玛乘,实际在处理时应该怎么处理?
- 虽说可以有4条路径到达,但是这些路径并不全是求和的形式,为啥可以直接写成全部相加的形式?
Reference
- https://blog.csdn.net/m0_74052450/article/details/145683491
- https://zhuanlan.zhihu.com/p/1930733342564807975
- https://cloud.tencent.com/developer/article/2109462
- Why LSTMs Stop Your Gradients From Vanishing: A View from the Backwards Pass (weberna.github.io)
- 【漫话机器学习系列】069.哈达马乘积(Hadamard Product)-CSDN博客
- 深度学习原理——-循环神经网络(RNN、LSTM)_深度学习原理 循环神经网络 rnn lstm-CSDN博客


