最优控制:在约束条件下达到最优的系统表现
- 约束条件是比较确定的,比如物理限制
- 最优的系统表现则是设计人员来确定的,比如自动驾驶中汽车转弯的快速性和舒适性,如何更好的达到两者的平衡
对于一个多目标相互约束问题,比如汽车变道,一方面要求轨迹误差尽可能小,另一方面要求侧向控制输入尽可能小(为了舒适度)。在这种情况下,定义一个代价函数$J$,该函数为误差和控制输入的加权线性组合,通过最小化这个代价函数来实现最优控制,通过调整加权值,可以调整我们更侧重于误差更小还是输入更小(即能耗更少或更舒适):
其中,$u,e$分别表示控制输入和跟踪误差,$q,r$权重用于调整系统的整体表现,如果$q>>r$,说明我们更看重误差,如果$r>>q$,说明我们更看重输入。对于上面公式所表述的最优控制来说,我们就是希望求出控制输入$u$,使得代价函数最小。对于多输入多输出系统,上述可以写为矩阵形式:
注:后面我们仅基于线性时不变系统进行讨论
MPC-模型预测控制
通过模型来预测系统在未来一段时间段内表现进行优化控制,实际使用中,系统模型都是离散型的状态空间表达$x_{k+1}=Ax_k + Bu_k$ 。模型预测控制的步骤分为三步:
在$k$时刻
Step1:估计/测量当前系统状态
Step2:基于来进行优化,此时代价函数就可以写成下面的形式:
- 其中最后一个项表示的是预测区间最后一个时间点的误差的代价函数,即我们除了希望整体的误差小,当然也希望一系列控制输入之后,最后时刻的误差能够变为0。我们需要求出控制序列来使上面的代价函数最小。
Step3:在 $k$时刻计算出来的最优化结果,在实施的时候只实施$u_k$这一步,而不是将所有控制序列依次实施,然后再重新求解。而是每次都实施最前面一个的控制序列,以新的时刻作为$k$时刻,再重复上述的计算,这个过程,叫作滚动优化控制
因为在每一步都有进行一次最优化的计算,所以MPC对控制器的计算能力要求较高。
二次规划
对于二次规划问题来说,它的一般形式如下:
即求出$Z$使上面的式子有最小值。处理上面这种二次规划问题现在已有很多现成的方案,所以我们要做的就是将模型预测控制的代价函数,转化为上述二次规划问题的一般形式,此时我们就可以求解最优的 $U_k$。
如何将问题转化为二次规划问题
假设有一个系统,其状态空间表达为:$x(k+1)=A x(k)+B u(k)$,其中$x$是一个状态向量,$u$是一个输入向量。先进行一些声明,在 $k$时刻:
- 在 $k$时刻预测的输入为 $u(k|k)$,在 $k$时刻预测的$k+1$时刻的输入为$u(k+1|k)$,在 $k$时刻预测的$k+2$时刻的输入为$u(k+2|k)$,以此类推到在$k$时刻预测的 $k+N-1$时刻的输入为$u(k+N-1|k)$,这里的 $N$被称作预测区间。
- 同理,对于系统的状态而言,在$k$时刻预测的系统状态记为 $x(k|k)$,在 $k$时刻预测的$k+1$时刻的系统状态为$x(k+1|k)$,以此类推,一直预测到$k+N$时刻,系统的状态$x(k+N|k)$。
- 注意输入是预测到 $k+N-1$时刻,系统状态是预测到$k+N$时刻,这是正常的,因为从系统的状态空间表达看,系统的$k+N$时刻的状态是由 $K+N-1$时刻的状态和输入计算出的。
将一段时间预测的系统状态和输入写为向量的形式:
- 系统状态:$X_k = [x(k|k),x(k+1|k),x(K+2|k),…x(k+N|k)]^T$
- 系统输入:$U_k = [u(k|k),u(k+1|k),u(k+2|k),…u(k+N-1|k)]^T$
为了方便,我们设系统的输入就是系统状态,即 $y = x$,参考值$R=0$,这样误差 $E=y-R=x$,简化推导,这个时候我们就可以得到代价函数:
其中说明如下:
- 为了简单$Q \ R \ F$均设为对角矩阵:

接下来需要将上面的代价函数转化为上述的二次规划问题,因为我们最终控制是控制输入$u$,所以我们要将$x$消掉,最后想办法化简成只有输入 $u$ 的二次规划问题。
设系统初始状态为 $x_k$,根据系统状态方程可得:
进一步化简得到:
记
式子可以化简为:
将代价函数打开,去掉求和符号得:
记
则代价函数可简记为:
又因为 $X_k = M x_k + C U_k$,将其带入上式得:
因为代价函数的值是一个值,所以对于上式中的
来说,这两个互为转置,且他们一定是一个值,所以这两个互为转置的表达是相等的,即
因此可以对代价函数再进一步化简得:
接着,我们记:
则代价函数就可以最终化为:
上式中除了$U_k$剩下的均为已知量,此时我们就将其转化为了二次规划问题的一般形式,然后就可以利用现成的方法求解$U_k$了。
维度问题
计算一下几个重要矩阵的维度。一般状态空间的离散表达为:
其中:
- 为 n X 1维矩阵, 为 n X n维矩阵, 为 n X p维矩阵, 为p X 1维矩阵
这样对于上面的推导我们可以知道:
为 (N+1)n X 1维矩阵
为 Np X 1维矩阵
为 (N+1)n X n维矩阵
对于矩阵C,需要知道矩阵中的0是0向量,比如左上角的0,它其实是nx1维的0列向量,因此我们可以知道C为 (N+1)n X Np维矩阵。
这样对于公式:
计算出来的维度就可以匹配上:(N+1)n X 1 = (N+1)n X n维 n X 1维 + (N+1)n X Np维 Np X 1维。
一个简单的模型仿真
系统离散状态空间表达为:
我们设:
Matlab进行仿真代码如下
MPC_test.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50% 清屏
clear;
close all;
clc;
% 第一步,定义状态空间矩阵
% 定义状态矩阵 A, n*n 矩阵
A = [1 0.1; -1 2];
n = size(A,1);
% 定义输入矩阵 B, n*p 矩阵
B = [0.2 1;0.5 2];
p = size(B,2);
% 定义Q矩阵,n*n 矩阵
Q = [1 0;0 1];
% 定义F矩阵,n*n 矩阵
F = [1 0;0 1];
% 定义R矩阵,p*p 矩阵
R = [0.1 0;0 0.1];
% 定义step数量k
k_steps = 100;
% 定义矩阵 X_K, n*k 矩 阵
X_K = zeros(n,k_steps);
% 初始状态变量值, n*1 向量
X_K(:,1) = [20;-20];
% 定义输入矩阵 U_K, p*k 矩阵
U_K = zeros(p,k_steps);
% 定义预测区间K
N = 5;
% Call MPC_Matrices 函数 求得 E,H矩阵
[E,H] = MPC_Matrices(A,B,Q,R,F,N);
% 计算每一步的状态变量的值
for k = 1 : k_steps
% 求得U_K(:,k)
U_K(:,k) = Prediction(X_K(:,k),E,H,N,p);
% 计算第k+1步时状态变量的值
X_K(:,k+1) = (A*X_K(:,k) + B*U_K(:,k));
end
% 绘制状态变量和输入的变化
subplot(2, 1, 1);
hold;
for i = 1 : size(X_K,1)
plot(X_K(i,:));
end
legend("x1","x2")
hold off;
subplot(2, 1, 2);
hold;
for i = 1 : size(U_K,1)
plot(U_K(i,:));
end
legend("u1","u2")MPC_Matrices.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24function [E,H] = MPC_Matrices(A,B,Q,R,F,N)
n=size(A,1); % A是n*n矩阵,得到n
p=size(B,2); % B是n*p矩阵,得到p
M=[eye(n);zeros(N*n,n)]; % 初始化M矩阵,M矩阵是(N+1)n*n的,
% 它上面是n*n个"I",这一步先把下半部分写成0
C=zeros((N+1)*n,N*p); % 初始化C矩阵,这一步令它有(N+1)n*NP个0
% 定义M和C
tmp=eye(n); % 定义一个n*n 的 I 矩阵
% 更新M和C
for i=1:N % 循环,i从1到N
rows =i*n+(1:n); %定义当前行数,从i*n开始,共n行
C(rows,:)=[tmp*B,C(rows-n, 1:end-p)]; %将c矩阵填满
tmp= A*tmp; %每一次将tmp左乘一次A
M(rows,:)=tmp; %将M矩阵写满
end
% 定义Q_bar和R_bar
Q_bar = kron(eye(N),Q);
Q_bar = blkdiag(Q_bar,F);
R_bar = kron(eye(N),R);
% 计算G,E,H
G=M'*Q_bar*M; % G: n*n
% 此处考虑后面矩阵运算的写法,所以写成这个形式,和公式中略有不同
E=C'*Q_bar*M; % M'*Q_bar*C; % C'*Q_bar*M; % E: NP*n
H=C'*Q_bar*C+R_bar; % NP*NPPrediction.m
1
2
3
4
5function u_k= Prediction(x_k,E,H,N,p)
U_k = zeros(N*p,1); % NP x 1
U_k = quadprog(H,E*x_k);
u_k = U_k(1:p,1); % 取第一个结果
end
仿真结果
先仿真一下没有控制输入的情况,看一下系统的响应。可以看到系统状态最后发散:
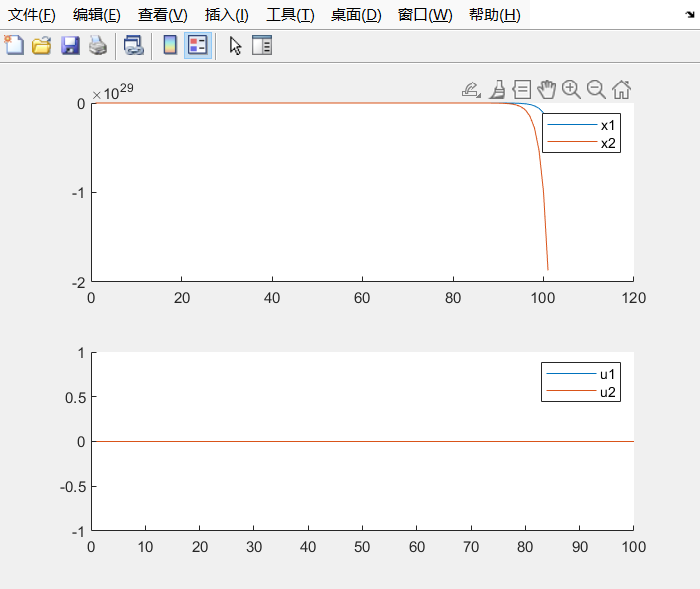
启用MPC控制,系统表现如下,系统能够稳定收敛:
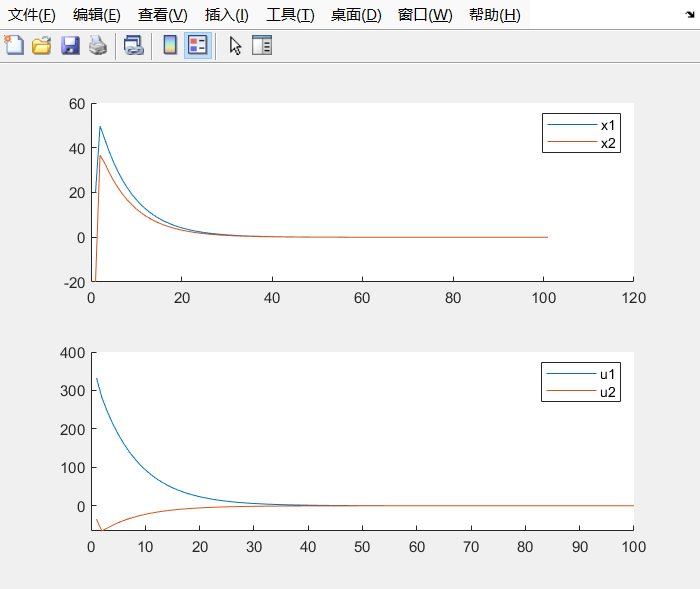
我们尝试修改:
- 程序修改如下:

- 即我们更加看重 的变化,此时得到的仿真结果如下,可以看到更快收敛,控制输入初始值也较大:
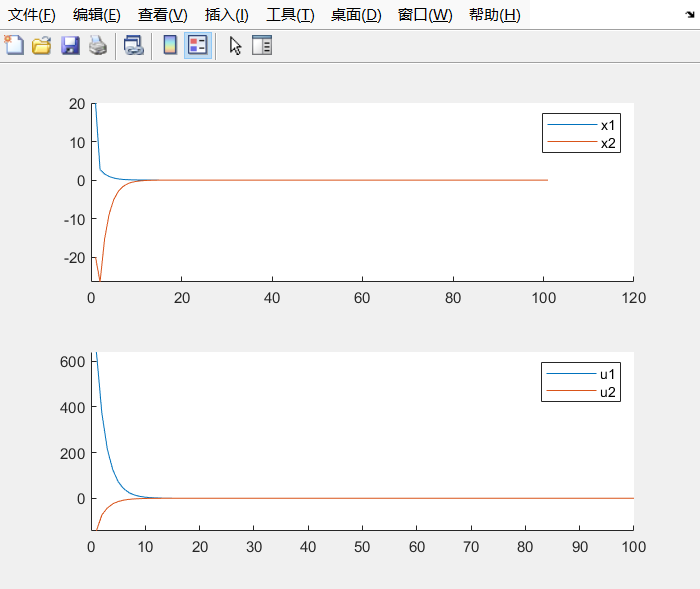
- 程序修改如下:
再次修改,上一次修改参数导致系统的 过高,我们希望系统输入不要过高,不然这意味着能耗变大,所以我们接着修改一下R矩阵,使被惩罚的更多。
- 修改如下:
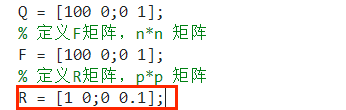
- 仿真结果如下,我们可以看到 的初始值小了一些同时变化也更平缓了。
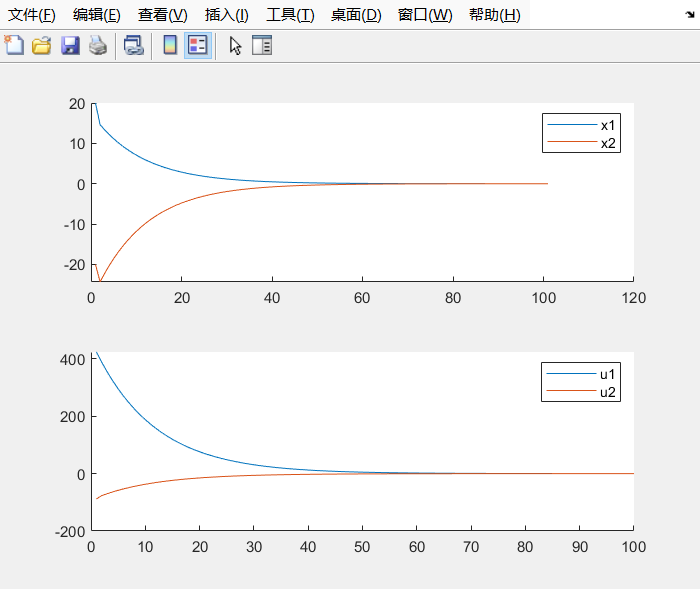
- 修改如下:
在实际使用中,我们就要根据实际情况来调节Q F R矩阵来达到我们想要的控制指标。


